275 (8)

10.3.4. Równania i nierówności logarytmiczne (I)

giiówno równanie, jak i nierówność (nic tylko logarytmiczne) we wstępnym etapie rozwiązujemy, wyko- I

jjtie same przekształcenia (por. 3.1.3., 3.2.2., 3.6.6., 3.8.2. i 10.2.2.).

afljitńj#

gjMianic logarytmiczne i nierówność logarytmiczna mają niewiadomą usytuowaną pod logarytmcm (ilijil naż\va), jako wyrażenie logarytmowane lub jako podstawa logarytmu (por. 10.2.2a.): przykład log₄(2x- 5) = 2,    log(, _ ₂\(x+ 3) = 2,

log₂(x- 3) + 16g₂(x + 1) < 3, log_i(x - 1) - log_i(x + 2) > 1,

• pmpadloi równania:

Przyrównujemy same wyrażenia logarytmowane (por. własność w 103.2e.), otrzymujemy równanie retanianowc lub wymierne (ewentualnie wykładnicze), które rozwiązujemy (por. 3.6.6.; 3.8.1. lab 1911).

Wżeramy z dziedziny równania logarytmicznego (Uczone wartości niewiadomej (x) i formułujemy odpowiedź.

. w>l»lna procedura rozwiązywania niektórych równań i nierówności logarytmicznych (por. 10.2.2b.):

(1) wyznaczanie dziedziny:

Sileży tu również pamiętać, że:

onicnie logarytmowane musi być dodatnie (*)

i podstawa logarytmu (o ile zależy od niewiadomej) musi być dodatnia i różna od 1 (•*).

ja przykład, aby wyrażenie: log/, ₊ z)^~j" miało sens liczbowy, nie wystarczy założyć, że mianownik

(i-1)jest różny od zera; należy ponadto zaiożyć, że: —— > 0 (*), jako wyrażenie logarytmowane, j(i+2>0 i x + 2    1 )(**), jako podstawa logarytmu.

(2)    sprowadzenie obu stron równania i nierówności do logarytmów o jednakowych (wspólnych) podsta-Hch po ewentualnym uprzednim zastosowaniu praw działań na łogarytmach, na przykład:

-zastąpienie sumy logarytmów logarytmem iloczynu (por. własność 1. w tabeli w 10.3.1 b.)

-zastąpienie różnicy logaiytmów logarytmem ilorazu (por. własność 2. w tabeli w 10.3. Ib.)

-zastąpienie iloczynu liczby i logarytmu logarytmem potęgi (por. własność 3. w tabeli w 10.3.1b.)

(3)    mając po obu stronach (równania czy nierówności) logarytm o tej samej podstawie, przystępujemy <toporównania wyrażeń logarytmowanych - opuszczając logaiytmy o wspólnych podstawach:

w przypadku nierówności:

Porównując same wyrażenia logarytmowane: albo zmieniamy kierunek nierówności na przeciwny (gdy podstawa ne(0;l)), albo zachowujemy taki sam kierunek nierówności, gdy podstawa a 1 (l; +oo) (por. własność w 10.3.2f.).

Otrzymaną nierówność wielomianową lub wymierną (ewentualnie wykładniczą) rozwiązujemy wraz z ilustracją na osi liczbowej (por. 3.6.6.; 3.8.1. lub 10.2.2.) i zawężamy zbiór rozwiązań do dziedziny nierówności logarytmicznej; formułujemy odpowiedź.

Uwaga: Niekiedy, w przypadku bardzo skomplikowanych wyrażeń logarytmowanych nie wyznacza się apfic/fe dziedziny na początku rozwiązywania, a dopiero na końcu. Po obliczeniu niewiadomych (x) sprawdza się, podstawiając, czy wyrażenia logarytmowane są dodatnie, czyli czy logarytmy mają sens licz-bwy-bywa to łatwiejsze niż rozwiązanie wstępnych założeń. Jednak nie wolno zapomnieć o końcowym sprawdzeniu, o którym była mowa powyżej.

t)liklad równań lub nierówności logarytmicznych to koniunkcja odpowiednio równań lub nierówności lo-ptytmicznych.

mmnummum

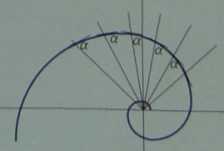
Spirala logarytmiczna

tet to rzut slercograficzny (podporządkowujący każdemu punktowi itf punkt płaszczyzny) loksodromy na płaszczyznę styczną z kulą 'punkcie biegunowym, niejako jej płaski sobowtór. Podobnie jak lok-**oma przecina wszystkie ziemskie południki pod tym samym kątem, ^spirala logarytmiczna tworzy takie same kąty ze wszystkimi swoimi Meńiamj wodzącymi. Różnica między tymi krzywymi polega na tym, '•pirala jest linią płaską, a loksodroma - przestrzenną.

10. FUNKCJE POTĘGOWE, WYKŁADNICZE I LOGARYTMICZNE