290 (33)

A =

-1

(XI 1.49)

Rys. XII.10. Reakcyjność

prędkości według [44]

462

Podstawiając (XII-41) i (XI 1.42) do (XII.40) znajdujemy

_ gc-iVn-g,)-rv?-2pv_tV l-g^COSZ,    (XI 1.44)

0—ff«A* |tf, + <r^ł(l-«_ł)+if-2f»_łV'|-f_łco»j,),

Jest to równanie przestępne, można je rozwiązać metodą numeryczną lub przybliżoną.

Oznaczając

e, - g<o+Aet, “ ^reO + A\ i zakładając małe przyrosty		(X11.45)
	(Aqc)^2 * 0, Aoe-Ave * 0	(X11.46)
oraz przyjmując	9 = <Po» *i ** *i®	(XI 1.47)
otrzymamy przybliżoną formę równania (XII.44)
	dvX . „dV,Tl Aqc — (1 — Qe0)— A — B— 1	(XII.48)
	*rO 1 ^rfO 1 ł

określającą zależność zmiany reakcyjności od zmiany wskaźnika prędkości:

Aq, =/(dv_e).

Występujące w równaniu (XI 1.48) stałe wynoszą:

2

((p-v_cj l-_Lvc°sa,-vf)₀

Przyjmując przykładowo <p₀cosa,₀ = °’⁹³⁵-

otrzymuje się współczynniki A, B jako funkcję reakcyjności obliczeniowej (rys. XII.9). Korzystając ze współczynników A, B według rysunku XII.9 obliczono za pomocą wzoru (XI (.48) reakcyjność w funkcji zmiany wskaźnika prędkości (rys. XII. 10).

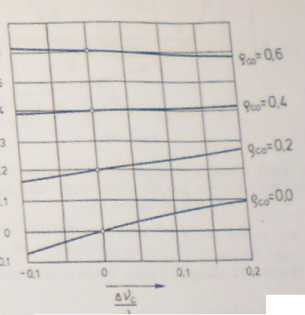
^veo

stopnia w funkcji zmiany wskaźnika

463

Dla niewielkich zmian wskaźnika V,, gdy

-0,1 < — < 0,2 v«o

(jak na rysunku XII.10), linie

/ <pcosg,\

v_e0

o_c(dv_c) można aproksymować prostymi

AQ_t = (0,5-Gco) (1 “<?«o)—• ^v*o

(Xll.50)