2a (84)

11. Metody wyznaczania przyspieszeń w ruchu płaskim.

Przyspieszenie dowolnego punktu bryły sztywne) w ruchu płaskim jest sumą geometryczną (wektorową) przyspieszenia ruchu postępowego bieguna, przyspieszenia stycznego (obrotowego) względem bieguna I przyspieszenia normalnego (doosiowago).

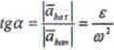
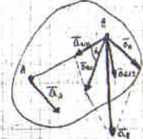
styczne:

a*, =*'■.

normaI:

a*. =tu‘T„

suma:

ós =ó. +ńfc,, +0*.

"* =ó. + «„

K| = >/K.|^ł +K-I’

12. Ruch kulisty cista sztywnego; kąty Eulera; precesja regularna.

Ruch kulisty to taki ruch dala sztywnego, podczas którego jeden jego punkt pozostaje nieruchomy (środek ruchu kulistego), W ruchu kulistym torami punktu ciała są krzywe, które lezą na powierzchniach kul o promieniach równych odleglośdom tych punktów od punktu nieruchomego.

z^ma*c ;&=£*£

X

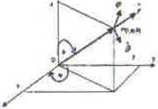
Precesja regularna to ruch. Jaki powstaje jeZell dało wprowadzimy w obrót z prędkością kątową wokół materialnej osi symetrii, a równocześnie osi symetrii nadamy ruch obrotowy dookoła osi w ustalonej przestrzeni.

13.    Prędkość I przyspieszenia w precesji tegularnoj.

Patrz pytanie (12).

14.    Ruch złożony (prędkość, przyspieszenie, przyspieszenie Coriollsa).

15.    Twierdzenie o składaniu prędkości.

Twierdzenie o składaniu prędkośd dotyczy wyznaczania prędkości ruchu płaskiego, traktowanego jako złożenie ruchu postępowego I obrotowego. Va « Vb ♦ Vab

01. Pojęcie punktu materialnego; prawa Newtona.

Punkt materialny to ciało o tak małych rozmiarach w porównaniu do obszaru w którym się porusza ze moZn8 pominąć zmiany położenia tego dala wyrażone przez obrót I traktować go jak punkt geometryczny. Punktowi przypisujemy pewną ilość masy.

I zasada dynamiki Newtona Punkt materialny (lub bryła sztywna) na który nie działają żadne siły lab siły te wzajemnie się równoważą, pozostaje względem układu odniesienia w spoczynku lub porusia się ruchem jednostajnym, prostoliniowym.