Zdjęcie0160 3

46kin

Wykład 7

Przyśpieszenie dowolnego punktu B pręta AB poruszającego się ruchem płaskim, jest równe sumie geometrycznej przyśpieszenia dowolnie obranego punktu A oraz przyśpieszenia punktu B wynikającego z obrotu względem punktu A.

Ruch kulisty ciała s/l>miei»n

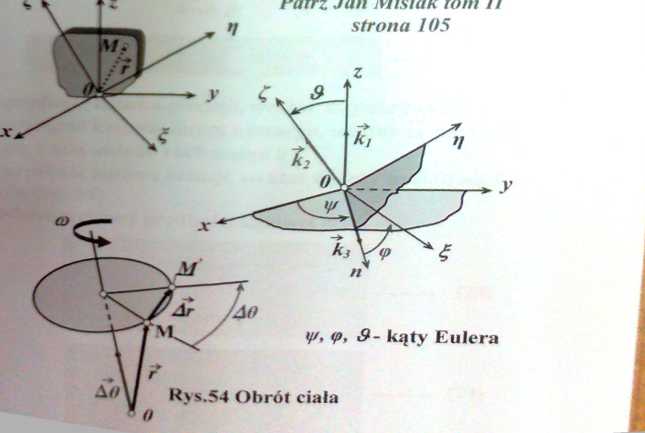
Ruchem kulistym ciała szty wnego nazywamy taki ruch ciała podczas którego jeden jego punkt pozostaje nieruchomy ksi, yr - psi, £ - d/cta. ę — fi, ą — eta, 3 - tej£a^ ^

Układ nieruchomy 6xyz, wersory tego układu iuji, ku układ zuiązaa> / ciałem wersory tego układu i₂,j2t k₂