312 (28)

312 -

Formalnie diagonalizację macierzy (4) można przeprowadzić znajdując jej wartości własne będące pierwiastkami równania charakterystycznego. Wtedy macierz D zostanie utworzona z wartości własnych macierzy i_<;1 natomiast macierz X z odpowiadających wektorów własnych.

Możliwy jest jednak inny sposób postępowania.

Równanie (4) można interpretować jako połączenie łańcuchowe trzech czwór-ników o macierzach łańcuchowych równych odpowiednio XfD.JP¹* Macierz łańcuchową diagonalną posiada idealny transformator o przekładni n^ a aia-nowicie

0

1

D =■

Możemy założyć, że macierz JC jest w postaci

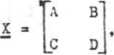
a ponieważ AD-3C = 1 dla czwórników odwracalnych, więc

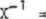
D -3

-C A_

Wobec tego otrzymamy Aę po wyznaczeniu jako

A

= m =>

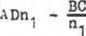
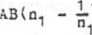
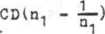
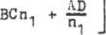
Na podstawie (6) i \4j dostaniemy:

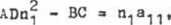
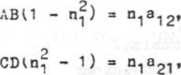
o

AD-BCn-j 0^22*

i

<j»orzyBtując zależność AD - BC = 1 oraz zakładając D =■ jlidnię transformatora i stałe czwórnika X:

otrzymamy prze-

22

(a

22

^a11>‘

- 1,

ⁿ1^a11 - ¹

T^'

W)

¹ - ⁿ1^a22

Z 18) 1 (3) oraz 15) wynika, że

Az

	An" - BCn"^n	AB(n~^n - n^a)		"^A11	^A12
a			=»
	C(n" - n"^n)	An"^n - BCn“		_^A21	^A22.

19)

Ze wzorów (8) wynika, że musi zachodzić Jn^ j 4 1. Przypadki, kiedy |n₁ j =1, są szczególne.

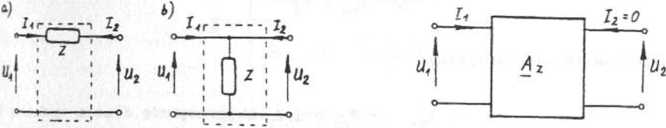
Rys. 3*66.2

Rys. 3.66.3

^?ak będzie na przykład wtedy, gdy czwórnik będzie miał postać taką jak na fjs. 3.66.2a i b. Jest to przypadek szeregowego lub równoległego połącze-impedancji. Można również zauważyć, że przekładnia transformatora ide-ilnego n₁ jest równa wartościom własnym macierzy A_<;. Z określenia perame-^{ró» macierzy łańcuchowej czwórnika oraz rys. 3.66.3 otrzymamy

^U1 ^A11

TT ⁼ ^T’

Mzi_e A.,, i A₂₁ obliczymy na podstawie 18) i (9).

(10)