351 (15)

j<y*

Relację (XIV. II5) można wykorzystać i rozbudować w rozmaity sposób. Przede wszystkim należy obliczyć siłę wieńcową (zwaną silą Thomasa) drogą całkowania elementarnej siły obwodowej za pomocą stosowanego założenia dla strat nieszczelności. Zazwyczaj stosowane wzory opierają się na liniowej zależności między stratą nieszczelności a wielkością szczeliny. Dzięki takiemu założeniu otrzymujemy liniowy związek między siłą wieńcową Q, a przemieszczeniem y:

(4)

fi, =

gdzie

oznacza współczynnik siły wieńcowej, P„ — całkowitą siłą obwodową przemiany bez strat, / — długość łopatek wirnikowych, K_s — współczynnik zależny od konstrukcji stopnia.

Podobnie uwzględnia się wpływ siły nadbandażowej (i siły w uszczelnieniu międzystopniowym):

Ogólnie, uwzględniając oba efekty, można napisać

fi * ry,

(XIV.l 16)

gdzie

(XIV. 117)

9 - q,+q_b ^{= K}~f

oznacza sumaryczny współczynnik siły wymuszającej. Wyraz K zależy od konstrukcji stopnia (przybliżone wzory na obliczenie współczynników q„ q_b i odpowiednie dane empiryczne podaje np. [47]).

Oznaczając

znajdujemy

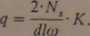
(XIV. 118)

Siła wymuszająca wynosi zatem

(XIV. 119)

5$8

Napiszemy wyrażenie na siłę tłumienia T(3) w innej postaci, wprowadzdj^Ł zamiast liniowego współczynnika tłumienia z dekrement logarytmiczny iłu-! mienia:

ii

M-to*

Wówczas

T = -M-(o£-y. n

(XIV.120)

Wstawiając (XIV.119) i (XIV.120) do warunku stabilności (XIV.l 15) otrzymujemy

n    d-l-co

stąd moc progowa, tj. moc wewnętrzna = tjf-N, odpowiadającagranłcj: stabilności układu, wynosi

1 9

Np rn

(XIV.121)

W tej postaci przedstawił Thomas wzór na moc progową. Napiszmy go w postaci odniesionej. Konkretna turbina ma moc znamionową wewnętrzną

I

N„ = t]_tmH_s.

Z równania ciągłości napisanego dla wlotu do kierownic

mW(j —    Cg,,,

po podstawieniu

'_0a ~ ^cio = utga, = -rntgaj,

wynika

1 _Jtd

m — —7rd/-cotgx₁,

stąd

N„ =nd²lo)tga_l. zv₀

Moc progowa odniesiona do mocy znamionowej wewnętrznej wynosi

(XIV.122)

Mu>l

fj =    ——B

^p N_n K it²-H_s dtga,