37 (69)

- 72 -

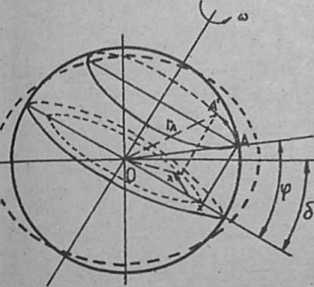
Dla dowolnej ezerokoici <f i kąta Ji wzniesienie pływu zrównoważonego jest okramiona równaniem /3d/_#przy. czym Z_M w tyfl równaniu jest połowy kęta wewnętrznego stożka , którego wierzchołkiem jest środek Ziemi,a tworzące prze* chodzi przez pozycję obserwatora na powierzchni kuli /por, rys* 2.7/# Rzut pozycji obserwatora na płaszczyznę równi* ka znajduje się w punkcie z'na linii łęczęcej środki Zle* el 1 Księżyca, a wlęct

/35/

OX* a ł» • cos <p • cos A

Zgodnls z definicję kęta Z_H Jest on określony przez

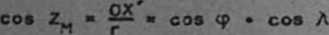
Ponieważ

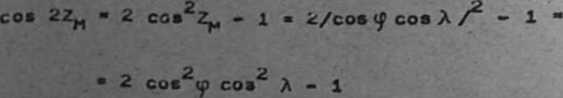
to równania /34/ przyjauja postać

* 5 |Ś    | 3/2ćos²q» cos² A - 1/ ♦ ^ł]

“ 5 | (§)" || coa²<p cos² A - ² ]    “

/36/

| a *    / 3 cos²9 cos² A — 1/

zrównoważone-

Równanie /36/ określa naa wzniesienie płv^wu go c dla dowolnych ssartoścl (f 1 A *

M

V

/

\

fr- 20*30'

0

Rys. 2.15. Maksymalna deklinacja Księżyca

Ne rysunku 2.16 przedstawiono wartości § dla szerokości O i o°, 30° i 60°. W cięgu Jednego obrotu Ziemi /A ■ 0 ~ 360°/ zarówno woda wysoka,jak i niska powtarzają się dwukrotnie. Taki pływ nazywamy pływem półdobowym. Maksymalne wahania pływu obserwujemy na równiku, które w miarę wzrostu szerokości geograficznej maleję.

Rozpatrzoy teraz przypadek drugi, gdy przyjmiemy maksymalna deklinację Księżyca w układzie Ziemia - Księżyc /£- 26,5°/. DIS niezerowych deklinacji Księżyca wzór /29/ staje się bardziej Płożony i ograniczamy się do koóconej postaci równaniat

-!;m' ■ § § (§) f/3sin²(p • sin² 5 -1/    *