43 (421)

94

Liczby zespolone

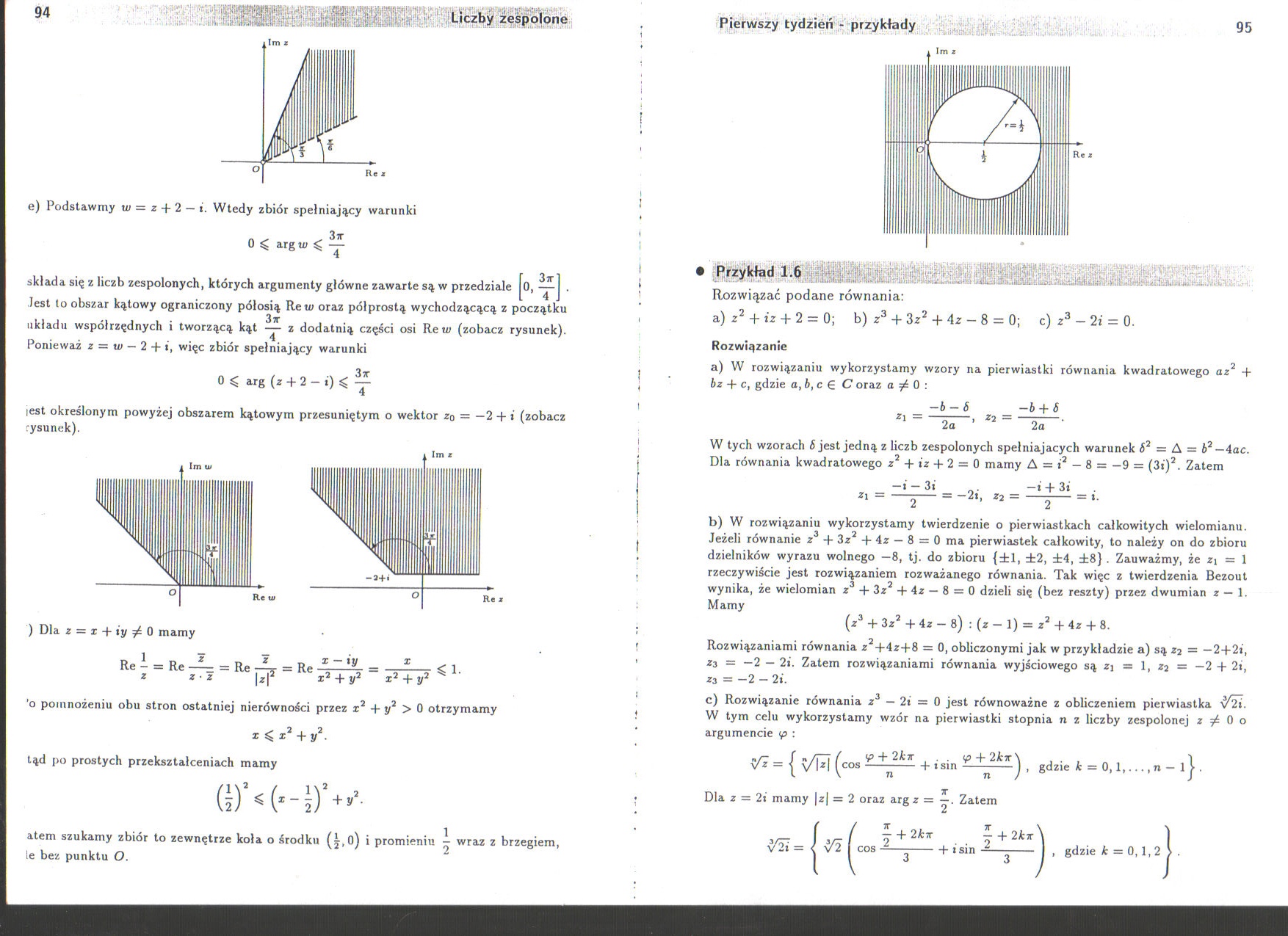
e) Podstawmy w = z + 2 — i. Wtedy zbiór spełniający warunki

0 arg w ^ ^

4

składa się z liczb zespolonych, których argumenty główne zawarte są w przedziale |o,    .

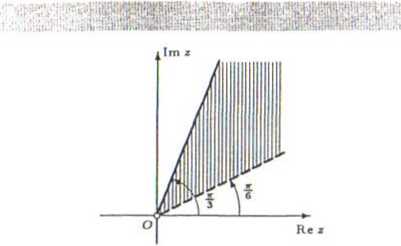
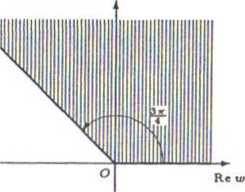
Jest to obszar kątowy ograniczony półosią Rem oraz pólprostą wychodzącącą z początku układu współrzędnych i tworzącą kąt — z dodatnią części osi Retu (zobacz rysunek). Ponieważ z = u> — 2 -f », więc zbiór spełniający warunki

0 $ arg (z + 2 — i) ^

4

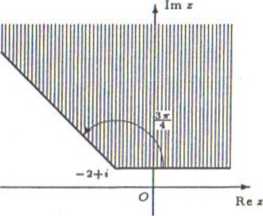
iest określonym powyżej obszarem kątowym przesuniętym o wektor zo = — 2 + i (zobacz rysunek).

Im w

) Dla z = z + iy ^ 0 mamy

Re - = Re ^Z _ = Re —= Re z    z • z

€ 1.

x - iy

|z|² i² + y² i² + y² 'o pomnożeniu obu stron ostatniej nierówności przez i² + y² > 0 otrzymamy

x $ z² + y².

ląd po prostych przekształceniach mamy

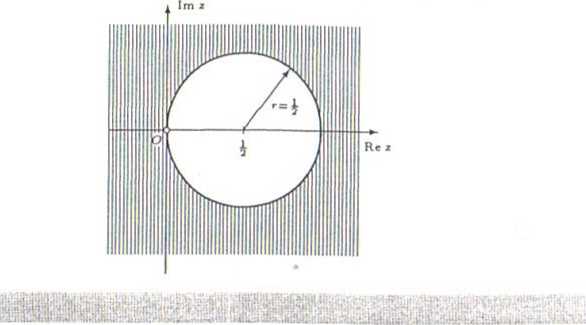
atem szukamy zbiór to zewnętrze koła o środku (j,o) i promieniu ~ wraz z brzegiem, le bez punktu O.

Pierwszy tydzień - przykłady

95

• Przykład 1.6

Rozwiązać podane równania: a) z² + iz + 2 — 0; b) z³ + 3z² + 4z - 8 = 0; c) z³ — li = 0.

Rozwiązanie

a) W rozwiązaniu wykorzystamy wzory na pierwiastki równania kwadratowego az² + bz -f c, gdzie a, b, c € C oraz a jŁ 0 :

Zl

—b — 2 a

6

*2 =

-b + S 2 a

W tych wzorach S jest jedną z liczb zespolonych spełniających warunek S² = A = b² — 4ac. Dla równania kwadratowego z² -f iz + 2 = 0 mamy A = i² — 8 = —9 = (3j)². Zatem

*i

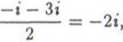
z₂ =

—i + 3i 2

i.

b)    W rozwiązaniu wykorzystamy twierdzenie o pierwiastkach całkowitych wielomianu. Jeżeli równanie z³ + 3z² -f 4z — 8 = 0 ma pierwiastek całkowity, to należy on do zbioru dzielników wyrazu wolnego —8, tj. do zbioru {±1, ±2, ±4, ±8} . Zauważmy, że z\ = 1 rzeczywiście jest rozwiązaniem rozważanego równania. Tak więc z twierdzenia Bezout wynika, że wielomian z³ -f 3z² + 4z — 8 = 0 dzieli się (bez reszty) przez dwumian z — 1. Mamy

(z³ -f 3z² + 4z - 8) : (z - 1) = z² + 4z + 8.

Rozwiązaniami równania z²+4z+8 = 0, obliczonymi jak w przykładzie a) są zi = — 2-f 2j, Z3 = —2 — 2». Zatem rozwiązaniami równania wyjściowego są z\ = 1, Zi = — 2 + 2i, z₃ = -2 - 2t.

c)    Rozwiązanie równania z³ — 2i = 0 jest równoważne z obliczeniem pierwiastka vĆ2i. W tym celu wykorzystamy wzór na pierwiastki stopnia n z liczby zespolonej r ^ 0 o argumencie ip :

sfz = { łj/fzj (cos    ą. isin ~~~~) ’ gdzie £ = 0,1.....n-l}.

Dla z = li mamy |z| = 2 oraz arg z = —. Zatem

f /    ^ + 2 kir

v^2j = < I cos ——--

+ : sin

i+2*,'

, gdzie A: = 0, 1,2