55 (306)

1.7. Kratownice

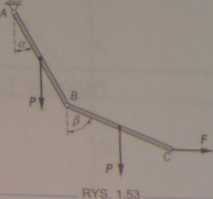
Dwa jednorodne pręty AB i BC są połączone przegubem B. Koniec A zamocowano na stałym przegubie. Na swobodny koniec C belki BC działa pozioma siła F równa połowie ciężaru P każdego z prętów. Znaleźć kąty a i fi w położeniu równowagi oraz reakcje R_A i Rg (rys. 1.53).

Odpowiedź
1 tg<* = 3-	k Iw 11
RAy=2P,	RBy = P

1.7

Kratownice

Kratownicą będziemy nazywać układ prętów, który zachowuje I się jak ciało sztywne. W tym punkcie zajmiemy się jedynie . kratownicami płaskimi. Kratownice rozwiązywać będziemy $ przy następujących założeniach upraszczających:

—    pręty są połączone przegubami (węzłami),

—    siły działające na kratownicę są przyłożone w węzłach,

—    ciężary własne prętów zaniedbujemy (względnie po-: łowę ich wartości zaczepiamy w węzłach),

—    tarcie w przegubach zaniedbujemy.

Aby kratownica dała się rozwiązać, musi być ona statycznie wewnętrznie i zewnętrznie wyznaczalna. Warunkiem koniecznym (ale niewystarczającym) na to, aby kratownica była statycznie wewnętrznie wyznaczalna jest spełnienie równości

p = 2w — 3

gdzie: p — liczba prętów, w — liczba węzłów kratownicy.

Statyczna wyznaczalność zewnętrzna wymaga, aby liczba niewiadomych reakcji zewnętrznych nie przekraczała liczby niezależnych równań równowagi.

Jedną z metod rozwiązywania kratownic jest analityczna metoda równoważenia węzłów. Metoda ta polega na tym, że rozpatrujemy równowagę każdego z węzłów osobno. Po myślowym odcięciu danego węzła od kratownicy otrzymamy układ sił zbieżnych w jednym punkcie i dla takiego układu możemy ułożyć dwa niezależne równania równowagi. Należy więc rozwiązywanie rozpocząć od tego węzła, w którym scho-

55

Zadanie 1.47