6

8. Planimetria, cz. 1. Wiadomości wstępne. Trójkąty

Twierdzenie Pitagorasa

Jeśli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.

a²+b²=c²

Twierdzenie odwrotne do twierdzenia Pitagorasa

Jeżeli długości boków a, b, c trójkąta spełniają zależność a²+b²=c², to trójkąt ten jest prostokątny, przy czym boki długości i są przyprostokątnymi tego trójkąta, a bok długości c - przeciwprostokątną tego trójkąta.

Twierdzenie o wysokości w trójkącie prostokątnym poprowadzonej na przeciw-prostokatna

W trójkącie prostokątnym wysokość poprowadzona z wierzchołka kąta prostego dzieli przeciwprostokątną na takie dwa odcinki, że wysokość ta jest równa pierwiastkowi kwadratowemu z iloczynu długości tych odcinków.

Twierdzenie o związkach miedzy długościami boków trójkąta a rodzajem tróikata ze względu na kąty

Niech a, b oraz c oznaczają długości boków trójkąta oraz a<b<c.

1) Jeśli a² + b²<c², to trójkąt jest rozwartokątny.

2) Jeśli a² + b²>c², to trójkąt jest ostrokątny.

Twierdzenie Talesa

Jeżeli ramiona kąta (lub ich przedłużenia) przetniemy dwiema prostymi równoległymi k oraz /, to stosunek długości odcinków wyciętych przez te proste na jednym ramieniu kąta (lub na ich przedłużeniu) będzie równy stosunkowi długości odpowiednich odcinków wyciętych na drugim ramieniu kąta (lub na jego przedłużeniu).

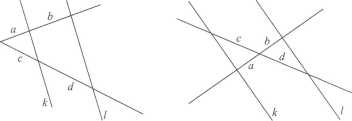
Jeśli £ ||/, to - = -.

b d

81