72 73 (12)

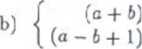
x -I- (q -f b + l)y = 2a + 1 Ir + (a — b)y = 4a² — 1

(a -b + l)x + (a — b)y = 4a² - 1 ' ^punkt- ^prOSta’ P^łaszczy^zna;

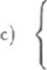
x - ay + bz = 3ab

x — ay - bz — ab

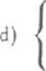
—ax -f by — cz — bc

ax + by -f cz = ab

x — ay + bz =. 2ab , punkt, prosta, płaszczyzna, przestrzeń;

—ax + by + cz = ab , punkt, prosta, płaszczyzna, przestrzeń ?

O Zadanie 7.6

Ułożyć układy równań liniowych o podanych zbiorach rozwiązań:

a) prosta w R³ o równaniu parametrycznym x = 4 -f t, y = 3 — 2f, z = 5,

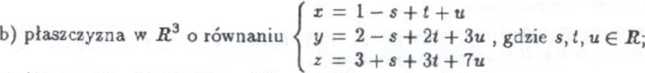
c)    {(i + 2«,3-4*,5 + &,7-80 : te R}\

d)    {(! + «- *,2+s + <,3-s + 2t,s + 2t,2*-0^: s,t 6 #};

e)    {(4 + 2s-rs + 3<,2 + s- ti,4-s-r2u) :    ii};

f)    {($ + 2t — u 4- v, 1 4- s 4- u — 3t) : s, t, ti, v E R}-

Odpowiedzi i wskazówki

7.1    a) wymiar 3, baza {(1,2, 0, 0), (0. 5,1,0), (0, 3,0,1)}; b) wymiar 1, baza {(0,0,1,-1)}; c) wymiar 2, baza {(1,0,1,0),(0,1,0,1)}; d) wymiar 1, baza {(1,-1,1, —1,1)]; e) wymiar 0; f) wymiar 2. baza {(-2,1,0,7), (-1,0,1,3)}.

7.2    a), c) nie; b) tak.

7.3    a) {(a + l,8a + l,5a + l): a € ii}; b) {(-4a + 36, 9a - 95 + 1,2a, 26) : a, 6 € ZZ};

c)    {(a + i + 5c+ l,-2a —26 —6c + l,a + M + l,c + l) _: a,b,c€Ji};

d)    { (a + j,b, 76 — 6a)    a,&€ii}.

7.4    a) płaszczyzna w ii³ o równaniu 2x — y + 4z + 3 = 0; b) prosta w Ji³ o równaniu x-fl5_y + 7

-23 ~~ -10

7.5* a) prosta dla a = 0 i 6 ^ 0, płaszczyzna dla a = b = 0;

b)    punkt dla a ^ prosta dla a = —, rozwiązania nigdy nie tworzą płaszczyzny;

c)    zbiór rozwiązań nie może być punktem ani całą przestrzenią, prosta dla a = 0 i b 0, płaszczyzna dla b = C, dla ab ^ 0 układ nic ma rozwiązań; d) punkt dla abc 0, prosta dla ac ^ 0 i b = 0 oraz bc ^ 0 i a = 0, płaszczyzna dla dokładnie dwóch spośród liczb a,b,c równych 0, cala przestrzeń dla a = 6 = c = 0, dla ab ^ 0 i c = 0 układ nie ma rozwiązań.

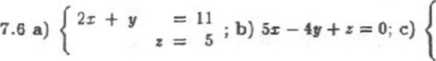
2x + y

3x

4x

— x

5

2 ;

+ u = 11

r^3z ■	rdzien - oc y + 2*	= 7
ti) { 4x	+ 3* —	u =13	e) 3z + y — 14r — 7t' = —44;
l 3x	+ x	— v = 6
f) 0 x + 0	y = 0.