74 (116)

słowne i liczby

rysunek konki .słowne i liczby

2ii 2ii

AA O OO OOOO OOOOOOO

^ZlC Zzt    7 2-1 (1) z;i pis slow no-liczbowy (określeniu słowne i liczby), up.:

/uda mc 4

Darek ma 6 książek. a Agam o 3 więcej. Ile książek ma Agata¹'

D. 6 ksia/ek

A. o 3 więcej, czyli 6 4-3

e) zapis liczbowy (wypisanie tylko lic/b / /.udania, ale takie ich ustawienie. abv widać było. które /. nich łączą sie w działania).

Po wykonaniu zapisów możemy przystąpić do rozbioru zadań jedną z wvbranych metod (lub wybór pozostawiamy uczniom).

Istotą rozbioru analitycznego jest myślowe rozłożenie zadania złożonego na zadania proste tednodziałaniowe. od wielkości nieznanych do znanych. Wykonujemy to na organigramach (drzewkach), interpretując słownie wykonywane operacje. Dochodzimy do schematów, z których łatwo określić pytania i działania łub ułożyć wzór ro/wią/nnia w jednym zapisie. A oto przykład schematu do zadania 2.

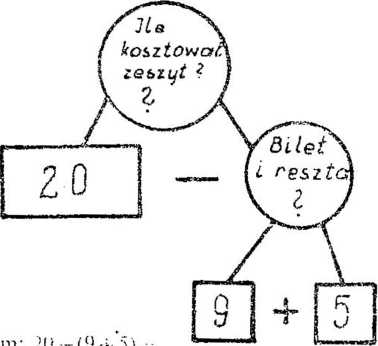
Rozwiązanie w/ore,,.. _w

Rozwiązanie pytaniami (/ zastosowaniem już me(odv anatiiyczno-synte-tycznej): Jaką kwotę stanowił bilet i reszta? 9-f-5-- 14

lic kosztował zeszyt'.’

Zalety metody analitycz-nęj: ks/talei myślenie uczniów poprzez prawidłowy lok rozumowania, rozwija słownictwo matematyczne uczniów i w metodzie lej trudno o biedy w rozumowaniu. Wady: zawiły i długi sposób rozumowania, w którym uczniowie łatwo mocą sic zgubić, dużo mewiadomycli w zadaniu, szukanie odpowiedzi bezpośredniej przez pośrednie niewiadome, tok rozwiązywania nie jest zgodny z tokiem rozumowania (gdyż odpowiada metodzie syntetycznej).

Rozbiór syntetyczny jest odwrotności;) analitycznego, przebiegającego ml wielkości znanych bezpośrednio poprzez wielkości pośrednie do wyniku. Schemat rozbioru do zadania 2 może być następujący:

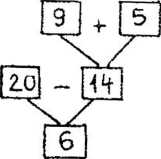
Rozwiązanie może być od razu na drzewku, ale można także rozwiązać zadanie za pomoc;) pytań (takich samych jak podałem przy poprzednim schemacie).

Zalety metody syntetycznej: prosta, jasna, dostępna dla uczniów, jedno działanie wynika z drugiego, niewiadoma jest tylko jedna, do której dążymy bezpośrednimi drogami bez pośrednich niewiadomych i jest zgodna / planem rozwiązania. Wady: w metodzie tej łatwo o błędy, bowiem uczeń nic zawsze dobierze odpowiednią parę liczb i nie potrafi ustalić działania między tymi liczbami.

Rozbiór metodą analityczno-syntetyczną polega na tym, że rozbioru dokonujemy sposobem analitycznym, a rozwiązujemy zadanie sposobem syntetycznym, za pomocą kolejnych pytań zc schematu (od dołu) i działań do nich. Metoda ta jest najbardziej przydatną i przystępną w początkowej fazie rozwiązywania zadań. Rozwija poprawne rozumowanie i język matematyczny.

Sposoby rozwiązywania zadań

Przez rozwiązywanie zadania tekstowego rozumiemy poszukiwanie drogi pozwalającej na wykonanie szeregu operacji ma tema tycznych.