bez tytułu15 (2)

226 Podstaw i mak rock anomii

c	y s0y
z ~	z z
c
—- z=	w — • w.
Z	o

(6)

Wstawiając do równania (6 ) równania (3) i (4) uzyskujemy:

(7)

= nf-dm.

Funkcja (7) osiąga maksimum, gdy pochodna tej funkcji względem ni jest równa zeru¹:

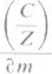
anf ¹ —d = 0.

(8)

Z równania (7) wyznaczamy d:

(9)

d— a*m^0_ *.

Podstawiając równanie (5) do równania (9) uzyskujemy:

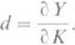
.    . bY

Ponieważ —-o K

dr

d K'

to możemy zapisać:

dł

d K

Konsumpcja na jednego zatrudnionego jest maksymalna, gdy stopa zużycia majątku produkcyjnego zrównuje się z krańcową produkcyjnością kapitału.

Zadanie 2

*r =

Air

gdzie Air = w, —w, ,,

¹ Jest to warunek konieczny. Warunkiem dostatecznym jest. aby druga pochodna funkcji (7) względem m była mniejsza od zera. Obydwa warunki są spełnione.