CCF20090421003 (3)

Grapa punktowa o symbolu: 222 zbiór nrerzący => (2,; 2,( (2,; 2^2^! }

Na podstawie podanego zbioru tworzącego i znajomości mnożenia macierzy można wyprowadzić tabelę grupową

Jest to grupa:

>    4~ro elementowa (rząd grupy 4)

>    niecykliczna

r przemienna, bo: 2_>®2_Z = 2_Z@22_X

	2.	2	^2i 1 ^1
2.	1	2,	i U
y	a	^1 1 i 5
2	2 )	2s	^1 !^21
I	^2.	^2,	mt-

S. A.R}t««S)fc-FaT4

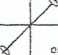
przecinają s:ę pod kątem 90⁼

Grupa punktowa o symbolu: mm2 zbiórtworzący => (m_r m,}

{ m_x; m_v; 2_Z, I }

Na podstawie podanego zbioru tworzącego i znajomości mnożenia macierzy można wyprowadzić tabelę grupową

Jest to grupa

>    4_ro elementowa (rząd grupy 4)

>    niecykliczna

>    przemienna, bo: m_>®2_z = 2_z€Jtn_v.=^t

s		"V	~2	i
	I	2	"S	mŁ
"V	2Z	1	mt	mv
2			ł	2.
1	m,	"V		1

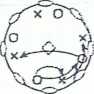
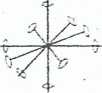
Grupa punktowa o symbolu: 422 zbiór tworząc* => (4/, 2j {4_Z; V;(= 2₂);4/; 4₇<(=i); 2_X; 2_}; 2_1;-; 2_{; jłi}}

2_fj- oraz 2₅._i0- symbole osi dwukrotnych zgodnych z kierunkami [HO] i £1-3OJ

(kierunki przekątnych między osiami X i Y okładu współrzędnych,. Wszystkie cs:e cztery dwukrotne prostopadłe do osi głównej przeć. s:ę pod karem 45* (lub jego wielokrotnośćrąj

Jest to grupa:

>    8-mio elementowa (rząd grupy 8)

>    niecykliczna

>    nieprzemienna, bo.

4,&2,*2,®4,

5. A RiiŁT^fc-Pirei

4. Grapy punktowe z główna osia obrotu i równoległymi do nićt płaszczyznami zwierciadlanymi X + m j j

X®mjj=> mm2 (2mm); 3m; 4mm; 6mm

W grupach tych seria płaszczyzn symetrii przecina się wzdłuz jednej prostej, która jest jednocześnie główną csią obrotu -każda z płaszczyzn zawiera tę samą prostą

5 AJo-WłMc-Firei.

Grupa punktowa o symbolu: 4mm zbiór tworzący => {4_lt m..} H_z; 4^=2_Z);V; V(=I); m_s; m>; m_u0; m.__ia}

m.j- oraz m_£_,_Ł - symbole płaszczyzn zwierciadlanych prosKpŁÓrycn do kierunków [ił0] i £1-10]

Płaszczyzny zwierciadlane przecinają się wząjemme pod kątem 45' (łub jego wielokrotnością)

^pr

P|-

^pr

'v

^p2

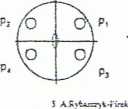
płaszczyzny przecinają s:ę pc-d kątem 90=

5 a