CCF20090522003

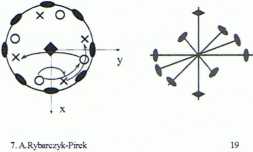
Grupa punktowa o symbolu: 422 zbiór tworzący => {4_Z; 2_X} oś główna (czterokrotna - 4_Z) i prostopadła do niej przynajmniej jedna oś dwukrotna {4_Z; 4_Z²;(= 2_Z );4_Z³; 4_Z“(=1); 2_X; 2^ 2₁₁₀; 2,.₁₀ }

2_n0 oraz 2,.,₀- symbole osi dwukrotnych zgodnych z kierunkami [110] i [1-10]

(kierunki przekątnych między osiami X i Y układu współrzędnych)

Wszystkie osie cztery dwukrotne prostopadłe do osi głównej przecinają się pod kątem 45° (lub jego wielokrotnością)

Jest to grupa:

>    8-mio elementowa (rząd grupy 8)

>    niecykliczna

>    nieprzemienna, bo:

4_Z® 2_X*2_X® 4_Z

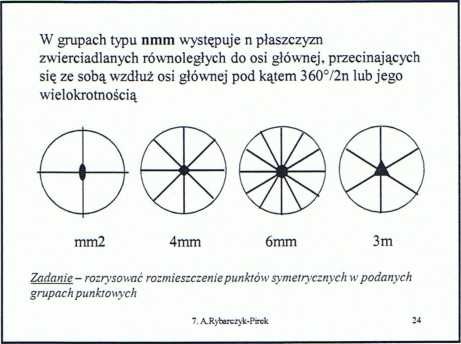
4. Grupy punktowe z główna osia obrotu i równoległymi do niei płaszczyznami zwierciadlanymi X + m j |

X ® m 11 => mml (2mm);    3m; 4mm;    6mm

W grupach tych seria płaszczyzn symetrii przecina się wzdłuż jednej prostej, która jest jednocześnie główną osią obrotu -każda z płaszczyzn zawiera tę samą oś obrotu (oś główna jest równoległa do każdej z płaszczyzn symetrii)

7. A-Ryberczyk-Pirek    21

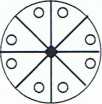
Grupa punktowa o symbolu: 4mm zbiór tworzący => {4_Z; mj oś główna (czterokrotna - 4_Z) jest równoległa do płaszczyzny symetrii {4_Z; 4_Z²;(= 2_Z );4_Z³; 4_Z⁴(=1); m_x; m_n0; m,.₁₀}

m,₁₀ oraz m,_₁₀- symbole płaszczyzn zwierciadlanych prostopadłych do kierunków [110] i [1-10]

Płaszczyzny zwierciadlane przecinają się wzajemnie pod kątem 45° (lub jego wielokrotnością)

Jest to grupa:

>    8-mio elementowa (rząd grapy 8)

>    niecykliczna

>    nieprzemienna

Zadanie - proszę sprawdzić, że jest to grupa nieprzemienna

7. A-Rybarczyk-Pirek    23

Grupa punktowa o symbolu: mm2 zbiór tworzący => {m^ iriy}; {m_x; 2_Z} oś główna (dwukrotna - 2J jest równoległa do płaszczyzny symetrii

Na podstawie podanego zbioru tworzącego i znajomości mnożenia macierzy można wyprowadzić tabelę grupową

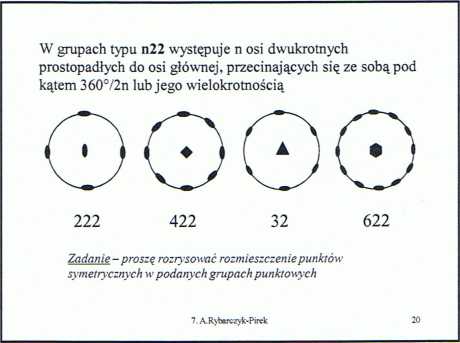
płaszczyzny przecinają się pod kątem 90°

P₂

P₄

{m,; ny 2_Z; 1 >

0	^mx	nij.	2Z	1
m*	1	2Z		m*
Hly	2Z	1	mx	my
2Z	niy		1	2Z
1			2Z	1

Jest to grupa:

>    4-ro elementowa (rząd grupy 4)

>    niecykliczna

>    przemienna, bo:

my02_z = 2_z®my= m*

4