CCF20090522�002

2_ m ’
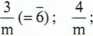
6_
m
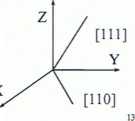
Według obowiązującej umowy w nomenklaturze krystalograficznej osiom obrotu zwykłym bądź inwersyjnym przypisuje się następujące kierunki:
h
3Z lub 3m [111]-kierunek przekątnej między osiami układu współrzędnych
6Z >
7. A. Rybarczyk-Pirek

Jest to grupa:
> 8-mio elementowa (rząd grupy 8)
> niecykliczna
> przemienna
Zadanie: proszą sprawdzić przemienność grupy
7. A Rybarczyk-Pirek

X<8>2 ±=> 222; 32; 422; 622
W grupach tych wszystkie osie obrotu przecinają się za sobą w jednym punkcie
Istnieją również grupy punktowe, w których występuje więcej niż jedna oś główna: 23 i 432.
Są to tzw. grupy regularne, opisujące symetrię wielościanów regularnych
7. A Rybarcz)k-Pirck 17
Na podstawie symbolu grupy wywnioskować można, że zbiorem tworzącym jest obrót o 180° i odbicie w płaszczyźnie prostopadłej do osi
obrotu np. {2y i nty}
By otworzyć całą grupę można wykonać tabelę mnożenia grupowego macierzy, lub posłużyć się rzutem stereograficznym.
Jest to grupa:
> 4-ro elementowa (rząd grupy 4)
> niecykliczna
> przemienna, bo: 2>.®my = my02ya: 1
{2^ 1; 1 }
|
® |
2y |
1 |
1 | |
|
2y |
1 |
r |
2y |
m, |
|
mv |
r |
i |
m, |
2y |
|
1 |
2y |
m, |
1 |
r |
|
f |
”V |
2y |
f |
1 |
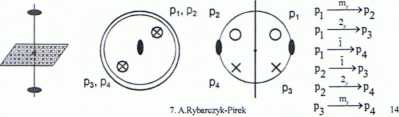
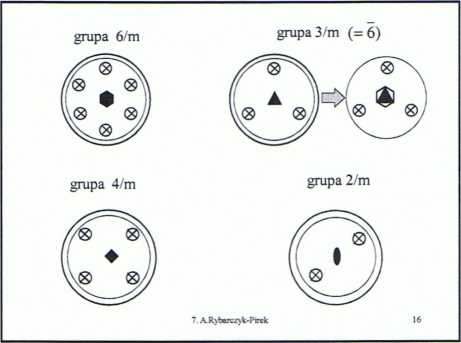
Grupa punktowa o symbolu: 222 zbiór tworzący => {2X; 2y} oś główna (dwukrotna - 2X) i prostopadła do niej przynajmniej jedna oś dwukrotna Na podstawie podanego zbioru tworzącego i znajomości mnożenia macierzy
{2,; 2,; 2*1}
można wyprowadzić tabelę grupową
osie 2-krotne przecinająsię pod kątem 90°

|
® |
2X |
2, |
2Z |
1 |
|
2X |
1 |
2> |
2y |
2X |
|
2y |
2Z |
1 |
2X |
2y |
|
2Z |
2y |
2X |
1 |
2Z |
|
1 |
2X |
2y |
2Z |
1 |
v
V
3
Wyszukiwarka
Podobne podstrony:
CCF20090522�004 5. Grupy punktowe główna osia obrotu, prostopadła do niej płaszczyzna symetrii, i ró
IMGH21 Założenie n.i piutt gdy dwie części drzewa m w płaszczyznach mc prostopadły
Slajd6 Wniosek: Ruchy punktów w płaszczyznach wzajemnie równoległych, a prostopadłych do osi ob
CCF20090421�000 (3) GRUPY PUNKTOWE Iloczyn dwóch operacji symetrii daje trzecią operację symetrii. K
CCF20090522�000 GRUPY PUNKTOWE Iloczyn dwóch operacji symetrii daje trzecią operację symetrii. Zawsz
FizykaII518�01 514 514 jeśli obie płaszczyzny odbicia są do siebie prostopadłe; dalej, że światło sp
CCF20090421�004 (5) W grapach typu nram występuje n płaszczyzn zwierciadlanych równoległych do osi g
CCF20091014�010 (3) <P rys. 8.7. Kąt obrotu względem siebie dwóch przekrojów prostopadłych do osi
CCF20090514�035 174 II. Struktura nauki spełnione) ceteris paribus. Głosiła bowiem, że na ramię pros
30938 skanuj0008 (90) Mx - moment względem osi x będącej równocześnie osią obrotu w stawie, 1 - licz
slajd08 (5) PŁASZCZYZNY PROSTOPADŁE Płaszczyzna P jest prostopadła do płaszczyzny a, jeżeli jest
więcej podobnych podstron