CCF20120509047

z. io ^/,ęst ii. nuzwią/.aiua i uupuwicu/.i

Położenie wektora naporu hydrodynamicznego R, czyli jego odległość od osi \, wyznaczamy z twierdzenia, iż moment siły wypadkowej względem dowolnego punku równy jest sumie momentów sił składowych, a więc

z. io ^/,ęst ii. nuzwią/.aiua i uupuwicu/.i

skąd

Re = R_xr — R₂r,

r(R₁-R₂)

e =

R

(KI

Po uwzględnieniu równań (6) i (7) oraz przekształceniach

e =

[n²pD⁴'d² — 8pQ²(D²—d²)~\(D² — d²)r [n² pD*d² + 8 pQ²(D² + d²)](D² + d²)'

3.3.5. W stanie równowagi, napór hydrodynamiczny R musi zrównoważyć cię/ai ścianki, czyli

(II

(2)

R = G.

a. Dla ścianki płaskiej (rys. II-3.14a):

R = pQc_v.

Prędkość c_y wyznaczamy z równania Bernoulliego, odniesionego do przekrojów 0 i 1:

w którym

2 g y    2 g    y

Po — Pl ⁼ Pb’

(')

zatem

(4)

c! = yJc²-2gH.

Podstawiając do zależności (2) wzór (4) oraz wiedząc, że

71D²

Q = —r-c,

otrzymamy:

nD²

G = R = p—c^c²-2gH,

(5)

skąd wysokość

H =

2 g

c² —

4 G

nD pcJ

(M

'"iil»l półkolistej (rys. 11-3.14b):

m)

1

8

4

,

::

I) i

///

i

i

!|

i!

.1

.00

R = pG[Ci-(-c₂)].

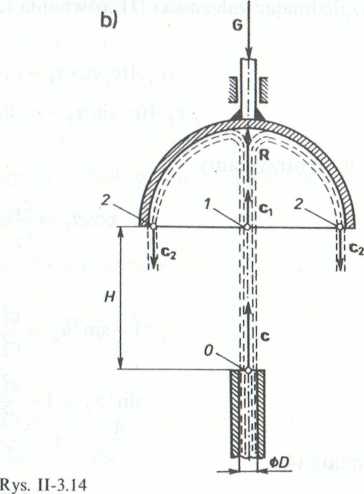
¹ , I < , wyznaczamy analogicznie, jak dla ścianki płaskiej, a zatem c, = c₂ = yj c^{1 2} — 2gH,

G = R = p-^-CyJ c² — 2gH,

nD²

' i oil iin,i wysokość H wynosi:

H =

1

2(7

2 G

nD² pc

1

III ,U,ulowi' naporu hydrodynamicznego wynoszą: R_x = pQ(c_lcosa._l — c₂cosa₂),

R_y = pQ(Ci sina! —c₂ sina₂),

2

,    11,, /iiii|iliijc siy w stanie równowagi to

R_r = 0,

R_y-G = 0.