CCF20120509061

itu ii. i\ua witania i uupumcuAi

Ponieważ

v = vV + i>„²,

zatem

v = a(x² + y²) 2.

Jednostkowe objętościowe natężenie przepływu

^ = <A(1,1) —iA(0,0),

czyli

0    3 a

6*2^a"2“° ^{= a}'

4.1.6. Poszczególne składowe pola prędkości wynoszą:

= x, v_y = -(y+t)

i spełniają równanie ciągłości

^ + ^ = 0 0x 0y

zatem

0iĄ

0X

= V_r = X.

0 ijj

0V

Całkując cząstkowo pierwsze z równań względem x, a drugie względem y otrzymamy:

iA(x,y,f) = xy + tx+f₁(y,t),

'A(x,.v,f) = x>’+/₂(x,t).

Z przedstawionych wyrażeń wynika, że /, może być funkcją tylko czasu f, gdyż w przeciwnym razie

#    5/1

0y    0y ’

01/f

0^⁼'^X’

a wtedy

01(/ 011/

0y * cy *

Wobec powyższego, z równań:

'A = xy + tx+f_l(t)

mii/

<P = xy+f₂(x,t),

oli/ymamy

./₂(x,0 = tx+f_l(t),

ulem funkcja prądu

ip = xy + tx+f_l{t),

i dla t = 1,

ip = xy + x+J\( 1).

1'ównunie linii prądu w chwili f = 1

ip(x,y, 1) = const,

i/yll    ^

xy + x+Jj(l) = const,

ili|il

x{y+1) = C.

( Mi /ymana zależność opisuje rodzinę hiperbol o asymptotach x = 0 i y = — 1 im II 4.2). Zwroty wektorów prędkości, stycznych do linii prądu i określających I li imick przepływu, wyznaczamy na podstawie składowych prędkości:

v_x = x, v_y= — (y + 1).

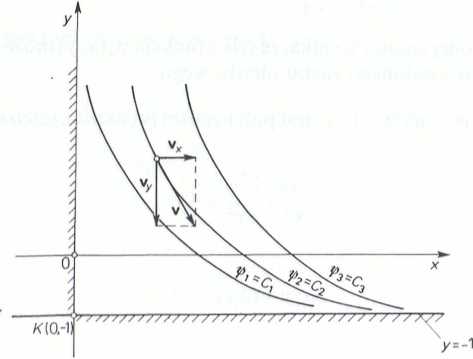
Rys. II-4.2