CCF20101004021

152 ii 8. Przedstawianie danych i graficzne oszacowanie hlęch

■l

papier z siatką, milimetrową., nazywany potocznie papierem milimetrowym (rys. 8.1A); papier z siatką, biegunową,;

- papier z siatką póllogaryliniczną, nazywany potocznie papierem pól-logarytmicznym lub papierem logarytmicznym (rys. 8.1C); papier z siatką logarytmiczną, nazywany potocznie papierem logarytmicznym, (rys. 8.ID).

W przypadku papierów z siatką póllogarytmiczną i logarytmiczną najczęściej przyjmuje się za. podstawę logarytmu 10.

Papier z siatką milimetrową ma charakter uniwersalny i jest najczęściej stosowany. Używany jest do różnego rodzaju wykresów, przede wszystkim wówczas, gdy spodziewamy się liniowej zależności między mierzonymi wielkościami, oraz gdy mierzone wielkości zmieniają się w zakresie mniej więcej jednego rzędu.

Papier z siatką póllogarytmiczną jest używany przede wszystkim wtedy, gdy spodziewamy się zależności typu:

y = ab^cx,

(przy czym a i c są stale i mogą być nieznane), ponieważ logi/ = logu -|-t:x log 6, a więc logi/ jest liniową funkcją x i wykres jest linią prostą. Stosuje się go również, gdy jedna z wielkości zmienia się znacznie (np. o kilka rzędów), a druga zmienia się parokrotnie.

Papier z siatką logarytmiczną stosuje się, gdy spodziewamy się zależności typu:

V

(siało a i b mogą. być nieznane), oraz gdy obie mierzono wielkości zmieniają, sio w zakresie paru rzędów.

Cfttośi -

4’

8.3.2.    jfiiisa dy.spo rządzai u ą._r w ykresów

Przed przystąpieniem do wykonania wykresu należy dokonać wyboru papieru funkcyjnego z odpowiednią siatką, pamiętając o tym, że w fizyce na ogól na osi odciętych (poziomej) odkłada się zmienną niezależną, a na osi rzędnych (pionowej) zmienną zależną. Następną czynnością jest dobranie skali. Wybierając skalę należy przestrzegać następujących reguł:

i    a) punkty doświadczalne nie mogą być zgrupowane na małym fragmen

cie rysunku (rys. 8.2A) i powinny pokrywać cały wykres (rys. 8.2B), a skala nie musi zaczynać się od zera;

ii

jj I)) skala powinna być możliwie prosta.

\

100 ■

V

80 -60 40 -20 0 -

A ⁶⁵ y

55-

dle

¹¹1¹¹¹1 ^{, t_}' i^{1 ri} i¹¹¹1 0    20    40    60    80    100

X

^{1 1} I

55

B

oio&rte

¹ i ^{1 1}

65

“I

75

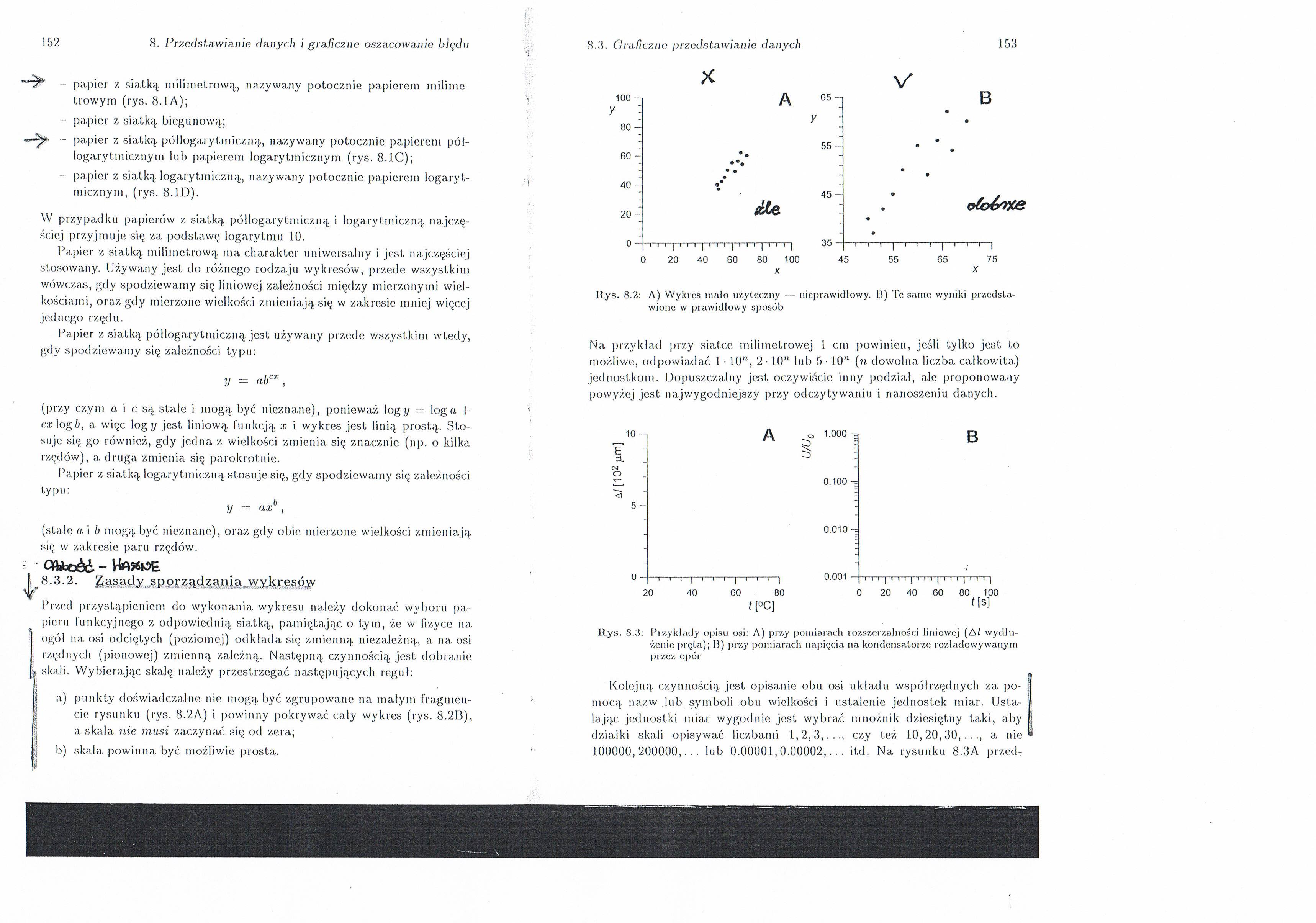
Rys. 8.2: A) Wykres mało użyteczny — nieprawidłowy. U) Te same wyniki przedstawione w prawidłowy sposób

Na przykład przy siatce milimetrowej 1 cm powinien, jeśli tylko jest to możliwe, odpowiadać 1 • 10^w, 2 • 10ⁿ lub 5 • 10ⁿ (n dowolna liczba całkowita) jednostkom. Dopuszczalny jest oczywiście inny podział, ale proponowany powyżej jest najwygodniejszy przy odczytywaniu i nanoszeniu danych.

A

I

1.000 -3

B

0.100 -

0.010 -

0--1—i—i—|—i—i—i—|—i—i—i—|

20    40    60    80

M°C]

0.001 - rr -p-i-ry. i i p

0    20    40    60

T¹

80

100

t[s]

Rys. 8.3: Przykłady opisu osi: A) przy pomiarach rozszerzalności liniowej (AZ wydłużenie pręta); B) przy pomiarach napięcia na kondensatorze rozładowywanym przez opór

Kolejną czynnością jest opisanie obu osi układu współrzędnych za po- \ mocą nazw lub symboli obu wielkości i ustalenie jednostek miar. Ustalając jednostki miar wygodnie jest wybrać mnożnik dziesiętny laki, aby i działki skali opisywać liczbami 1,2,3,..., czy leż 10,20,30,..., a nie* 100000,200000,... lub 0.00001,0.00002,... ild. Na rysunku 8.3A przed-