CCF20101004023

156 8. Przedstawianie danych i graficzne oszacowanie blęd

Nanoszenie granic błędów punktów pomiarowych jest konieczne, gdy wy-stępują odstępstwa od przewidywań teoretycznych. Przypadek taki przedstawiono na rysunku 8.5. Zaznaczanie błędów pomiarowych, gdy wszystkie pomiary są. obarczone tym samym błędem, może być ograniczone do jednego punktu, w przeciwnym razie należy zaznaczać błędy dla wszystkich punktów. W przypadkach gdy nanoszenie błędów nie wnosi żadnych informacji, nic nanosimy ich, ponieważ zaciemniałyby jedynie wykres. Zasady sporządzania wykresów zostały bardzo przystępnie przedstawione w [7] rozdział 11 (patrz także [10, 13, 19]).

8*4. Graficzne oszacowanie błędu

Nie należy do rzadkości odczytywanie danych z wykresu. Dane odczytujemy z wykresu wówczas, gdy nie możemy dopasować do wyników pomiarów zależności funkcyjnej metodą najmniejszych kwadratów, omówioną w rozdziale 3.5. Sytuacja taka może wystąpić na. przykład przy kalibracji przyrządów, czy też wtedy, gdy błąd żadnej z mierzonych wielkości fizycznych nie może być pominięty (por. rozdział 3.5 i 5.4). W dalszym ciągu tego rozdziału zajmiemy się przypadkiem, gdy zależność między mierzonymi wielkościami fizycznymi jest dana jedynie w postaci wykresu. Ponieważ wielkości mierzone bezpośrednio są. obarczone błędem pomiarowym, wobec tego i wykreślona krzywa, też będzie obarczona błędem. Powoduje to, że wartość odczytana z wykresu będzie również obarczona błędem. Błąd ten można oszacować graficznie. Graficzne oszacowanie błędu polega na oszacowaniu błędu wykreślonej krzywej, a następnie na. ocenie błędu wielkości odczytanej z wykresu.

Przedstawione poniżej graficzne oszacowanie błędu jest niezależne od tego czy na wykresie zaznaczono błędy maksymalne, czy odchylenia standardowe; w opisie wykresu musi to być jednak wyraźnie zaznaczone. Należy jednak zaznaczyć, że na ogół graficznie oszacowujcni)' błąd maksymalny.

8r4ri*. Oszacowanie błędu wykreślonej krzywej

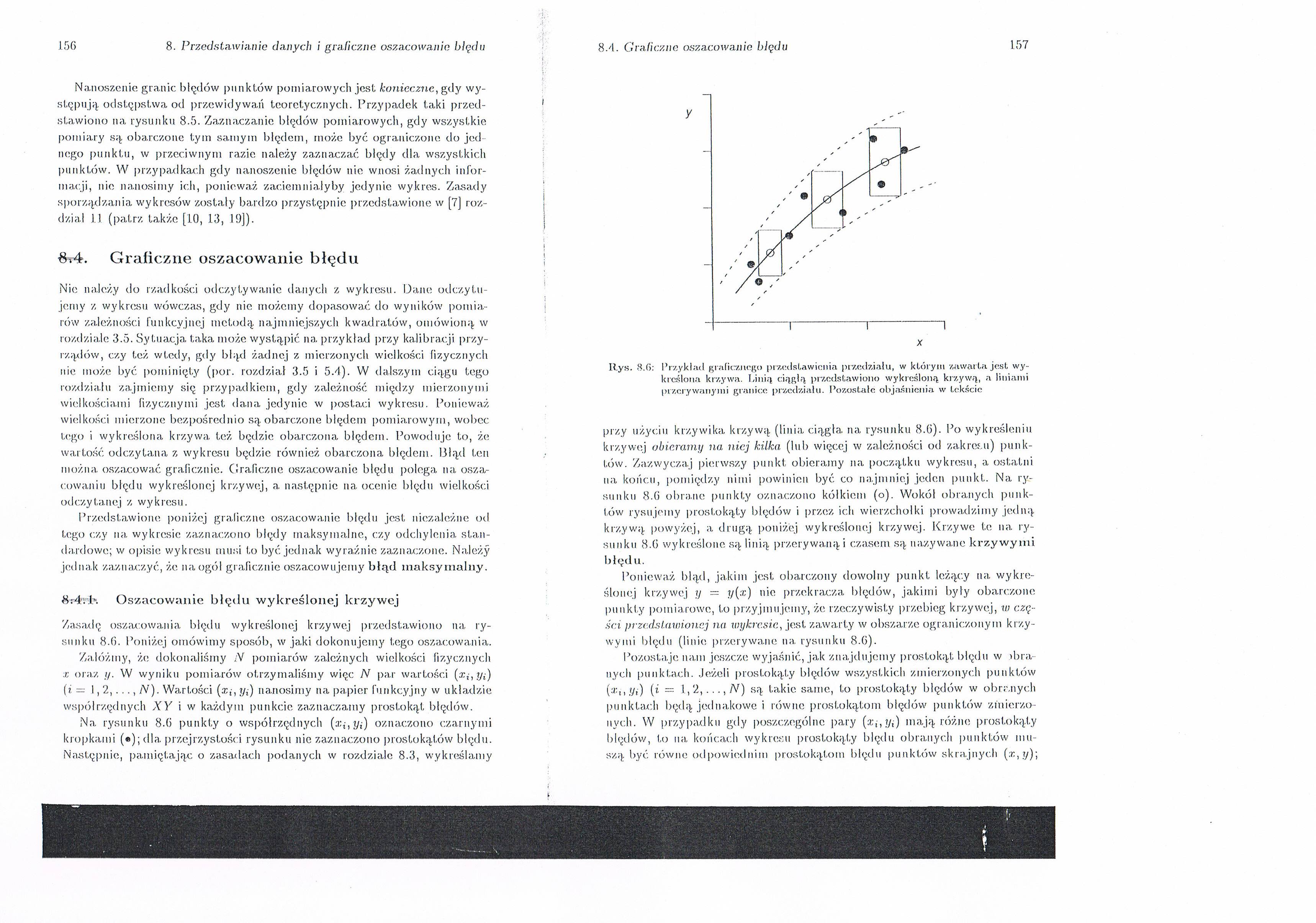
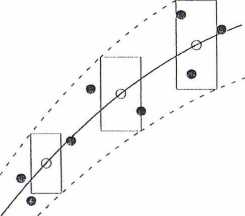
Zasadę oszacowania błędu wykreślonej krzywej przedstawiono na rysim ku 8.6. Poniżej omówimy sposób, w jaki dokonujemy tego oszacowania.

Załóżmy, że dokonaliśmy /V pomiarów zależnych wielkości fizycznych x oraz y. W wyniku pomiarów otrzymaliśmy więc N par wartości (x_t-, ?y_t) {i = 1,2,..., N). Wartości (®j, yi) nanosimy na papier funkcyjny w układzie współ rzędnych X Y i w każdym punkcie zaznaczamy prostokąt błędów.

Na rysunku 8.6 punkty o współrzędnych y*) oznaczono czarnymi kropkami (®); dla przejrzystości rysunku nie zaznaczono prostokątów błędu. Następnie, pamiętając o zasadach podanych w rozdziale 8.3, wykreślamy

y

X

Rys. 8.6: Przykład graficznego przedstawienia przedziału, w którym zawarta jest wykreślona krzywa. Linią ciągłą przedstawiono wykreśloną krzywą, a liniami przerywanymi granice przedziału. Pozostałe objaśnienia w tekście

przy użyciu krzywika krzywą (linia ciągła, na rysunku 8.0). Po wykreśleniu krzywej obieramy na niej kilka (lub więcej w zależności od zakresu) punktów. Zazwyczaj pierwszy punkt obieramy na początku wykresu, a ostatni na końcu, pomiędzy nimi powinien być co najmniej jeden punkt. Na rysunku 8.0 obrane punkty oznaczono kółkiem (o). Wokół obranych punktów rysujemy prostokąty błędów i przez ich wierzchołki prowadzimy jedną krzywą powyżej, a drugą poniżej wykreślonej krzywej. Krzywe te na rysunku 8.0 wykreślone są linią przerywaną i czasem są nazywane krzywymi błędu.

Ponieważ błąd, jakim jest obarczony dowolny punkt leżący na wykreślonej krzywej y — y(x) nie przekracza błędów, jakimi były obarczone punkty pomiarowe, to przyjmujemy, że rzeczywisty przebieg krzywej, w części przedstawionej na wykresie, jest zawarty w obszarze ograniczonym krzywymi błędu (linie przerywane na rysunku 8.0).

Pozostaje nam jeszcze wyjaśnić, jak znajdujemy prostokąt błędu w >bra uycli punktach. Jeżeli prostokąty błędów wszystkich zmierzonych punktów //,) (i = 1,2,..., N) są takie same, to prostokąty błędów w obranych punktach będą jednakowe i równe prostokątom błędów punktów zmierzonych. W przypadku gdy poszczególne pary (z;,!/;) mają różne prostokąty błędów, to na końcach wykresu prostokąty błędu obranych punktów muszą być równe odpowiednim prostokątom błędu punktów skrajnych (,r,y);