CCF20101004022

1.54 8. Przedstawianie danych i graficzne oszacowanie błędu

stawiono przykład opisu osi na papierze funkcyjnym z siatką milimetrową, a na rysunku 8.3)3 z siatką póllogarytmiczną.

Na tak przygotowany papier funkcyjny nanosimy punkty doświadczalne. Punkty doświadczalne muszą być zaznaczone wyraźnymi symbolami (np. •, X, o, *) tak, aby były dobrze widoczne. Jeżeli nanosimy na wykres punkty otrzymane w różnych warunkach, czy dla różnych próbek, to muszą one różnić się symbolami. Na wykresach powinny być zaznaczone niepewności pomiarowe. Można je zaznaczać na przykład za pomocą symboli:

lub

H lub	e
-	_

Prostokąt taki nazywamy prostokątem błędów.

Na ogól, gdy dla jednej wartości zmiennej niezależnej wykonujemy szereg pomiarów zmiennej zależnej, wówczas na wykres nanosimy ich średnią arytmetyczną lub średnią ważoną. W niektórych przypadkach, gdy chcemy przedstawić rozrzut wyników pomiarów, nanosimy wszystkie zmierzone wartości. Na. wykresach nanosimy zasadniczo błąd maksymalny. W przypadkach gdy nanosimy odchylenia standardowe serii lub średniej serii musimy to wyraźnie zaznaczyć w opisie rysunku.

Każdy rysunek musi być zaopatrzony podpisem, w którym podajemy, jaką zależność on przedstawia.. Oprócz tego podpis pod rysunkiem musi zawierać objaśnienie stosowanych symboli. Jeśli są one wyjaśnione w tekście, do którego dołączony jest rysunek, to nie musimy ich powtarzać, ale należy to zaznaczyć w podpisie, zamieszczając odpowiednią formulę, np.: Objaśnienia w tekście. W przypadku gdy do tekstu jest dołączonych kilka rysunków z tymi samymi oznaczeniami, to należy objaśnić je na. pierwszym rysunku, na. którym one występują, a na następnym można zamieścić uwagę: Oznaczenia jak na rys...

W celu pokazania, przebiegu badanej zależności pomiędzy punktami, doświadczalnymi prowadzimy krzywą gładką • „na oko” ....... używając krzy

wika., albo jeśli znamy postać zależności funkcyjnej, to znajdujemy ją metodą najmniejszych kwadratów. Przeprowadzając krzywą przy użyciu krzywika powinniśmy się starać, aby na każdym odcinku krzywej liczba punktów po prawej i lewej stronie, była. możliwie jednakowa, oraz aby krzywa, przechodziła. jeśli nie przez wszystkie, to przez większość prostokątów błędu.

I>RUn kj.ów,clośvviądę^ą.lny.ch jęsl..niejira,w^-dloyu^ Ponieważ każdy pomiar jest obarczony jakimś błędem, rozrzut wyników pomiarów jest rzeczą naturalną i łączenie poszczególnych punktów może sugerować skokowy charakter zależności, co nie zawsze ma miejsce. Jeżeli jednak podejrzewamy skokowy charakter zależności, to musimy zagęścić punkty pomiarowe. Na rysunku 8.4A przedstawiono nieprawidłowy wykres z linią, łamaną, zaś na rysunku 8.4B wykres prawidłowy z linią gładką poprowadzoną przy użyciu krzywika.

X    Y

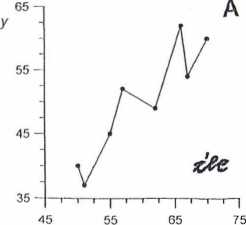
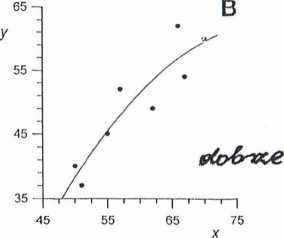
Rys. 8.4: Prowadzenie linii na wykresie: A) nieprawidłowe, punkty pomiarowe połączone linią łamaną; 13) prawidłowe

Często zdarza się, że na wykresie przedstawiamy porównanie przewidywań teoretycznych z wynikami pomiarów. Wtedy albo nie zaznaczamy punktów obliczonych i prowadzimy linię, albo muszą, się one bardzo wyraźnie odróżniać od punktów doświadczalnych. Zazwyczaj nie nanosi się punktów obliczonych, a prowadzi się linię. Tak samo postępujemy w przypadku dopasowywania funkcji do danych doświadczalnych metodą, najmniejszych kwadratów.

x    x

Rys. 8.5: A) Naniesienie granic błędów sugeruje zgodność wyników z poprowadzoną krzywą; 13) to samo, ale błędy mniejsze, odchylenie od krzywej wskazuje na istotne różnice