CCF20101004023

156 8. Przedstawianie danych i graficzne oszacowanie błędu

Nanoszenie granic błędów punktów pomiarowych jest konieczne, gdy występują odstępstwa od przewidywań teoretycznych. Przypadek taki przedstawiono na rysunku 8.5. Zaznaczanie błędów pomiarowych, gdy wszystkie pomiary są obarczone tym sa.ruym błędem, może być ograniczone do jednego punktu, w przeciwnym razie należy zaznaczać błędy dla wszystkich punktów. W przypadkach gdy nanoszenie błędów nie wnosi żadnych informacji, nic nanosimy ich, ponieważ zaciemniałyby jedynie wykres. Zasady sporządzania wykresów zostały bardzo przystępnie przedstawione w [7] rozdział 11 (patrz także [10, 13, 19]).

8*4. Graficzne oszacowanie błędu

Nie należy do rzadkości odczytywanie danych z wykresu. Dane odczytujemy z wykresu wówczas, gdy nie możemy dopasować do wyników pomiarów zależności funkcyjnej metodą, najmniejszych kwadratów, omówioną w rozdzi ale 3.5. Syt nacja taka może wystąpić na przykład przy kalibracji przyrządów, czy też wtedy, gdy błąd żadnej z mierzonych wielkości fizycznych nie może być pominięty (por. rozdział 3.5 i 5.4). W dalszym ciągu tego rozdziału zajmiemy się przypadkiem, gdy zależność między mierzonymi wielkościami fizycznymi jest dana jedynie w postaci wykresu. Ponieważ wielkości mierzone bezpośrednio są obarczone błędem pomiarowym, wobec tego i wykreślona krzywa też będzie obarczona błędem. Powoduje to, że wartość odczytana z wykresu będzie również obarczona błędem. Błąd ten można oszacować graficznie. Graficzne oszacowanie błędu polega na oszacowaniu błędu wykreślonej krzywej, a. następnie na ocenie błędu wielkości odczytanej z wykresu.

Przedstawione poniżej graficzne oszacowanie błędu jest niezależne od tego czy na wykresie zaznaczono błędy maksymalne, czy odchylenia standardowo; w opisie wykresu musi to być jednak wyraźnie zaznaczone. Należy jednak zaznaczyć, że na ogól graficznie oszacowujemy błąd maksymalny.

8r4rb. Oszacowanie błędu wykreślonej krzywej

Zasadę oszacowania błędu wykreślonej krzywej przedstawiono na rysunku 8.6. Poniżej omówimy sposób, w jaki dokonujemy tego oszacowania.

Załóżmy, że dokonaliśmy N pomiarów zależnych wielkości fizycznych x oraz y. W wyniku pomiarów otrzymaliśmy więc N par wartości (z,-, ty,) {t = 1,2,..., N). Wartości (z,-, t/;) nanosimy na papier funkcyjny w układzie współrzędnych X Y i w każdym punkcie zaznaczamy prostokąt błędów.

Na rysunku 8.6 punkty o współrzędnych (z;,t/,j oznaczono czarnymi kropkami (®); dla przejrzystości rysunku nie zaznaczono prostokątów błędu. Następnie, pamiętając o zasadach podanych w rozdziale 8.3, wykreślamy

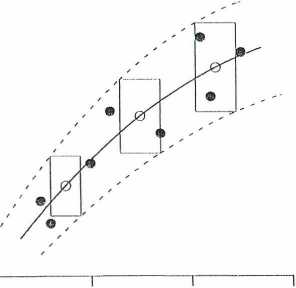
Rys. 8.6: Przykład graficznego przedstawienia przedziału, w którym zawarta jest wykreślona krzywa. Linią ciągłą przedstawiono wykreśloną krzywą, a liniami przerywanymi granice przedziału. Pozostałe objaśnienia w tekście

przy użyciu krzywika krzywą, (linia ciągła, na rysunku 8.6). Po wykreśleniu krzywej obieramy na niej kilka (lub więcej w zależności od zakres.u) punktów. Zazwyczaj pierwszy punkt obieramy na początku wykresu, a ostatni na końcu, pomiędzy nimi powinien być co najmniej jeden punkt. Na rysunku 8.6 obrane punkty oznaczono kółkiem (o). Wokół obranych punktów rysujemy prostokąty błędów i przez ich wierzchołki prowadzimy jedną krzywą powyżej, a drugą poniżej wykreślonej krzywej. Krzywe te na rysunku 8.6 wykreślone są linią przerywaną i czasem są nazywane krzywymi błęd u.

Ponieważ błąd, jakim jest obarczony dowolny punkt leżący na wykreślonej krzywej y = y(x) nie przekracza błędów, jakimi były obarczone punkty pomiarowe, to przyjmujemy, że rzeczywisty przebieg krzywej, w części przedstawionej na wykresie, jest zawarty w obszarze ograniczonym krzywymi błędu (linie przerywane na rysunku 8.6).

Pozostaje nam jeszcze wyjaśnić, jak znajdujemy prostokąt błędu w >branych punktach. Jeżeli prostokąty błędów wszystkich zmierzonych punktów (a;_t, fji) (i = 1,2,..., N) są takie same, to prostokąty błędów w obranych punktach będą jednakowe i równe prostokątom błędów punktów zmierzonych. W przypadku gdy poszczególne pary (:*:,, ?/,) mają różne prostokąty błędów, to na końcach wykresu prostokąty błędu obranych punktów muszą być równe odpowiednim prostokątom błędu punktów skrajnych (.r,jy);