CCF20101004020

150 8. Przedstawianie danych i graficzne oszacowanie błędu

Tabela 8.2: Przykład tabeli statystycznej

Zestawienie wyników pomiarów stałej grawitacyjnej G otrzymanych w latach 1990-1996 [20]

Au torzy	G [10““	m^3	s ^1 kg >]
Muller i inni (1990)	6.689	±	0.027
Zuiriberge i inni (1991)	6.677	±	0.013
Schurr i inni (1991)	6.66	±	0.06
Yang i inni (1991)	6.672	±	0.040
Schurr i inni (1992)	6.6613	±	0.0011
Oldham i inni (1993)	6.671	±	0.015
	6.703	±	0.035
Walesch i inni (1994)	6.6724	±	0.0015
Walesch i inni (1995)	6.6719	±	0.0008
Fitzgerald i Armstrong (1995)	6.6656	±	0.0006
Hubier i inni (1995)	6.678	±	0.007
	6.669	±	0.005
Meyer i inni (1995)	6.6685	±	0.0007
Fitzgerald (1995)	6.6659	±	0.0006
Midiaclis i inni (1995/96)	6.71540	±	0.00056
	6.7174	±	0.0020
Bagley i Lulher (1996)	6.6739	±	0.0011
	6.6741	±	0.0008

b)    w przypadku braku danych teoretycznych chcemy przewidzieć typ zależności funkcyjnej między mierzonymi wielkościami lub gdy chcemy ustalić zależność empiryczną między dwiema wielkościami, jest to przypadek występujący szczególnie często przy kalibracji przyrządów pomiarowych;

c)    chcemy graficznie wyznaczyć wartość jakiejś wielkości (współczynnika) występującej w zależności funkcyjnej (ten sposób w związku z rozwojem metod komputerowych jest coraz rzadziej stosowany);

d)    wyznaczonej zależności funkcyjnej nie można przybliżyć żadną prostą zależnością (np. pętla histerezy), w tym przypadku wykres stanowi ostateczną formę przedstawienia wyników;

c) badamy rozkład wyników pomiarów w danej serii, sporządzamy wtedy histogramy omówione w rozdziale 4.

8.3.1. Najczęściej używane papiery funkcyjne

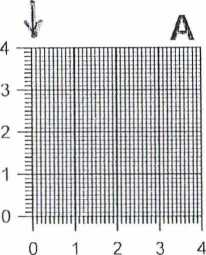
Wykpisy wykonuję sic na tzw. panicze riiiikcv.iiiy.iip Na papier funkcyjny jest. zawsze naniesiona odpowiednia siatka. Siatkę stanowi układ nadrukowanych linii, między którymi zachodzą związki zależne od rodzaju siatki, np. siatka milimetrowa składa się z dwóch prostopadłych do siebie układów linii prostych równoległych o odległości między liniami 1 mm. Istnieje wiele rodzajów siatek, wybór określonego rodzaju siatki jest zależny od analizowanej zależności funkcyjnej. Szczegółowe omówienie różnych siatek, zasady tworzenia i posługiwania się nimi można znaleźć np. w [21] (patrz także [13]).

ti/2 B

Rys. 8. L: Przykłady papierów funkcyjnych cJo sporządzania wykresów. Siatka: A) liniowa, 13) biegunowa, C) pól logarytmiczna, 1)) logarytmiczna

Najczęściej używane rodzaje, papierów funkcyjnych przedstawiono na rysunku 8.1, należą do nich: