CCF20130109009

W statyce oprócz siły korzysta się z innej wielkości, jaką jest moment siły względem punktu. Momentem siły P względem punktu 0 nazywamy wektor M₀ równy iloczynowi wektorowemu

M~₀=OAxP,    (1.1)

gdzie OA jest wektorem łączącym punkt A zaczepienia siły P z punktem 0, względem którego liczymy moment.

1.2. REDUKCJA DOWOLNEGO UKŁADU SIŁ

Każdy układ sił działający na dane ciało sztywne można zastąpić innym układem sił, równoważnym statycznie. Dwa układy sił nazywamy równoważnymi, jeżeli mają równe wektory główne i momenty główne względem dowolnego punktu.

Rozpatrzmy ciało sztywne obciążone siłami będącymi w równowadze, jak pokazano na rysunku 1.3.

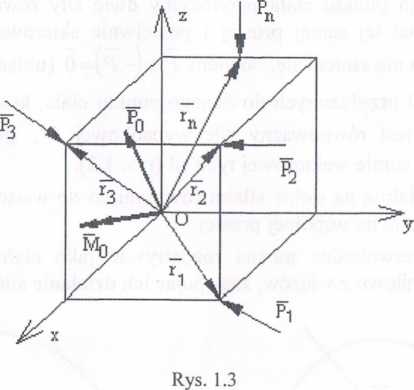
Wektorem głównym P₀ danego układu sił nazywamy sumę geometryczną wszystkich sił układu

ń =    (1.2)

;=i

Momentem głównym M₀ układu sił nazywamy wektor równy sumie geometrycznej momentów wszystkich sił układu względem punktu 0

M₀ =X^_to =XK^x/^)-

(1.3)

M    /=1

Redukcja układu sił polega na tym, że zastępujemy dany układ innym, statycznie równoważnym układem, złożonym z wektora głównego P₀ i momentu głównego M_n liczonego względem bieguna redukcji 0.

Rozróżniamy cztery przypadki redukcji układu sił: a) układ zerowy (P₀ - 0 , M₀ = 0), h) para sił (P₀ = 0 , M₀ ^ 0 ),

c)    układ złożony z wektora głównego (P₀ * 0, M₀ = 0 ),

d)    układ złożony z wektora głównego i wektora momentu głównego (P„ ź 0,

M₀ *0).

1'RZYKŁAD 1

Na bryłę o wymiarach podanych na rysunku 1.4 działają siły /} i P₂ . Zredukować dany układ sił do punktu 0 (0,0,0).

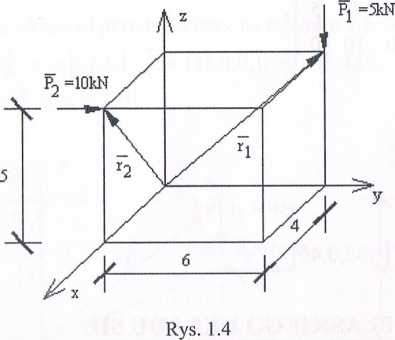
M Indowe poszczególnych wektorów wynoszą odpowiednio: /; [0,0,-5],    ^ = [0,6,5],

/'. [0,10,0],    V₂ = [4,0,5].