c��ki i pochodne2

J Odx = C

| dx-X-r C

f xdx = ~ x² +C

«+l

f x* dx — ——h C

^J    /7+1

ji<k=J*-'«fc=ln|x|+C

f«**₌.£L_+c

•    llltf

\e^xdx=e^x + C | sinxdx = -cosa: + C | cos avZv = sin .r + C | !gxdx ^In [cos :rj + C | ctgxdx = lnjsin x| * C

J -"7" ~ ^!£^x+ C

^J cos“x

r dx    _

J “7 2 ⁼ ~CtgX+ C

*    sin' ,v

dx

■,---= arcsin .v + (

³

r    dx    x

—=== = arcsin — + C

■    H

'1

!jT7^=arc^^+c_ 1

I \fa² -x dx~ —arcsin t^-+ — yfa² -x^: + C

^j    2 W 2

J

dx = —arcsin — — >4a -x +C

2 U 2

[    = lnjx + \(v^: 4- a

³ yf?~    ^r

\/.v“ + a

-1

Jctgⁿxdx =--ctg^{n l}x—jctg^{n 2x}xdx

+ C

\

.v

»2

W-0 [s}=nx"-'

W-1

1

n

COS X

^;r x

--i--

^4 2

+ C

J ln xdx = x(ln x -1)+C

|ln² xdx = x(ln² x-21nx + 2)+C

r dx    1    x -

—-Y = -<*rctg—+C

^Ja~+x    a    a

/

J r~5 2

Vx -a

r dx 1    1+

^Jl-x² 2    1-

^/x

+ C

| —jĄ=-dx=~-Jx² + n ~ ~InU + V.v‘ + a\ + C

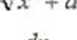
f yfp + adx = ~ V-v + a + — lnj.r + \/.v~’ + n * 2 2 ■

• a -x a •

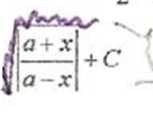
I sin" x<ix*= - -•sin’¹"¹ xcosx+ - fsin" “ xdx n    n ^J

J    ^ _ J

I cosⁿxdx - -sinxcos*"¹ .t +-1 cos" ²xdx

^J    n    n ^J

J tg"xdx = -itg"-²xJx

um

2 - t x ^ f

i W .    1

1/<*S "3-

'Uf*

X

i

X

M=-V-

2 vx

wvx

		“ 1 “
		.Va.

= ln(x +    ) + C

= ln(x + a/x² - a~ ) + C l+x

+ C

[sin x\= cosjc [cos x]= - sin .v

[&4=—^[—=l+tg²x

COS A"

[c/g^]'= —rV- = -(l + c/g^J.v)

Sl“ “ **

[arcsin x|=

sin" x

1

| arcsin xdx = x arcsin x + V l-x

J arccos xdx = x arccos x -yjl-x²

J arctgxdx = xarctgx -—ln li^x² |^C

J arcctgxdx = xarcctgx+ln(l + x²) + C

^/w^^=lnl^/(x)l^+c

j^=²V?w₊c

f[rwr/-c*)*-

_J/wT

« + l

+c

Vl-.v²

[arccos aJ=

VI-A²

[arctgx]= —1_

1+A"

[arc6’/g.v]'=

l+x²

A

a

[lnxj= —

X

f —--¹ — = ln|lnx +C ^J xlnx

[log, -^vl'= ~—

.v ln a

'"J^{1 + X}A-;

.r*}= x^x(lnx + l)

^T'^{1 1}

1

i-a²

a² + a¹ |I=

[ln(x-f \Lx²- a¹ j

Va- a²

_n *(<i)    *

Z ^se

6nx^(o)~ o')n (fc-t-n-j)

CCDX^hr CcC)( V+0*^J

-O

[A* yf'