120423

I Całki Riemanna: 1. i

J(e* —l)*e*dx

0

2.

jr xdx

J(x²+1)²

3.

rl+lnx ,

-dx

J x

1    *

5.

i;

dx

+ cosx

6.

x

2

4.

Jcos⁵ xsin2xdx

o

7.

r dx \ 2x² +3x —2

f xdx

*• ter

i

9.    Jxe~*dx

o

x

r xdx

10.    J-

ci

8.

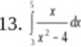
e^2xdx 1 -f-e*

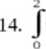
15.

SUl X

¹¹J

•J~xd x

4 >/x —1

V xdx

¹²- /:

o l-ł-Vx

rsin 2x o cos³ x

dx

16.

°r    3 dx

14x² + 4x—3

II Zbadać zbieżność całek niewłaściwych.

1.	"ędx i*^2	5.	‘ >111 xdx 2 X
2.	1 *	6. ?	dx
3. Ą	°ędx f ^	J i , 7.	xVx^2 —1 Je^dx
f	dx	8.
J .	k* -ł-2x-+-2	f	(arcrgx)^2 dx
		J	l-hx^2

f xdx	13.	> dx
		■J x ln x
f xdx	14.	dx
o Vl —X^2 | dx	f
	l*	:Vx—1 i
^ cos^2 2x	15.	f x ln xdx

12.

r dx

T Wx² -1

ODPOWIEDZI

I

1.			2	, 2	1 . 21
0,2(e —l)^5		6.	— 9. 7	e	13. -ln — 2 5
2	1	7.	0,2 ln — io. 3	e* —2	14.
	4			5	e^2 -1+ln——
3.	3 2	8. 1	11. . 4+>/T7 iW2 *	7 +2-J2 5	1 + e 15. 2(>/2—1)
4.	e —>/e	2		— 2In2 3	16. 3,„i
5.	2				8 9
1.	zbieżna do 1		7. zbieżna do 2		7T
2.	rozbieżna		1 3		12. zbieżna do —
3.	rozbieżna		8. zbieżna do — TC 12		13. rozbieżna
4.	zbieżna do TT		9. rozbieżna do + oo		14. zbieżna do TT
5.	rozbieżna		10. zbieżna do 1		1
6.	zbieżna do —		11. rozbieżna do + oo		15. zbieżna do —-4
	2