172 2

342 XVII. Całki funkcji niewymiernych

Łatwo obliczyć, że

= ln\x-\+\j x²-2x\.

dx

y/x²-2x

Mamy więc ostatecznie

J(3x-2)\!x²-2x dx=(x²-%x-\)\]x²-2x-\\n\x-l +'Jx²-2x\+C Zadanie 17.48. Obliczyć całkę

0)

dx

^x* y/5x² +2x—3 ’

Rozwiązanie. Jest to całka typu

(2)

I-

dx

^a)" \f ax² + bx+c

którą przez podstawienie -—u sprowadzamy do całek typu

x—a

(3)

f—

J h u¹

^xdu

+ ku+l

Rozważamy daną całkę w jednym z przedziałów: bądź x< -1, bądź x>f. Mamy a=0. Podstawiamy l/x = t, czyli x = l/t, skąd dx= -dtjt², gdzie — 1 </<0 lub 0</<|. Po podstawieniu mamy

i.

'V?4-³

Przy upraszczaniu postaci tego wyrażenia musimy pamiętać, że w pierwszym przypadku, tj. przy x<— 1, czyli — l<f<0, jest —t=\ft², a więc całka 7 jest równa

(4)

_r - f <*^dt

¹ J V5 + 2f—3f² '

W drugim natomiast przypadku, tj. przy x>f, czyli 0 < I < f, jest t = \ft², a więc całka /jest równa

(5)

r -fdt J V5 +2t — 3t²

vvię°

Ponieważ funkcje podcałkowe w całkach (4) i (5) różnią się znakiem, wystarczy obliczyć jedną z nich, np. pierwszą, tj. /,.

Całkę h obliczamy metodą współczynników nieoznaczonych, jak w. zadaniu 17.46;

flirt!    _4j

(6)

f -    ' ^ ——(at³ +ht² 4-ct + d)\/5 4-2l — 3t² 4- A f ^dt

J \l5+2t — 3t²    J V5+2f-3p

Różniczkując obie strony otrzymujemy

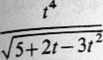
=(3at² + 2 bt +c)>j5+2t-3t² +

2_

+(at³ + bt² +ct +d) —,    +A ■

2\^/5 +2f — 3t²    V5+2t-3t²’

Mnożąc obie strony równości przez \I 5 + 2t — 3t² otrzymujemy

t⁴=(3flt²+2bt+c)(5+2r-3r²)+(ar³ + br²+cr+d)(l-30+/l =

= - 12nr⁴+(7a -9b) t³ +(15a + 5b - 6 c) r² + (106 +3c - 3 d) t+(5c+d+A). Przyrównując współczynniki przy jednakowych potęgach t otrzymujemy

1 =	— 12a ,	skąd	^a=~T2’
0=	la — 9b ,	skąd
0 =	15n+ 5b—6c,	skąd	c—S.
0 =	lOb +3c — 3d ,	skąd	d=-211 ^U 324 ’
0=	5c+ d + A ,	skąd	A- lii ^A 81 *

di

Pozostaje do obliczenia całka

dt

V5+2/-3r² >/3 J

Wykonujemy podstawienie t—$ = u, skąd dt-du, i według wzoru (17.2.4) otrzymujemy

/ - ¹ f *L ¹

³ V3J

,    1    3r-l

arcsin ^u=—~ arcsm-

⁴    V3    4

Wracamy do równości (6) i korzystając z uzyskanych wyników otrzymujemy

_r -l ,    ,    /-,    145    . 3r-l „

A = — (27z³ +21r² + 85t +155)y/S+21-3f² +    arcsin —— + C .

' +2x —3    145    . 3 —x

--1—:—7=. arcsm —--h C .

Stawiając t = l/x wracamy do zmiennej x; po przekształceniach otrzymujemy — 155x³ —85x² —21x—27

81 73

324x^J

4*