DSC00047 (26)

jeśli A zmienia się z temperaturą, to wykres temperatur staje się nieliniowy; przy a rosnącym z temperaturą wykres staje się wygięty ku górze /rys. Jo - II/, przy A malejącym z temperaturą - wygięty ku dołowi /krzywa III/ • Praktycznie można przyjmować dla ściany jednorodnej, że średni współczynnik przewodnictwa równa się średniej arytmetycznej, wartości A przy temperaturach t^ i

^Am

H ⁺ *2

-2-

/12/

2.1.3. Przewodzenie ustalone przez ściankę rury

Niech ciepło przenosi się przez ściankę rury o promieniu wewnętrznym r_w i promieniu zewnętrznym r_z. Weźmy pod uwagę

różniczkowy pierścień w ściance rury, pierścień o promieniu r i grubości dr. Proces przenikania cie -pła przez ten pierścień, zgodnie z prawem Fouriera, wyrazi się wzorem

q = -A . 2TS.1. H gdzie 1 - długość rury.

ściankę rury.

Bye.4, Przewodzenie przez

* ^{dt B} r:hri * ¥

Po scełkowsnlu ostatniego równania w granicach r_z i r_w otrzymujemy

/13/

t_ 11.

2511

/1V

Po pomnożeniu i podzieleniu prawej strony ostatniego równania przez r_z - r_w otrzymujemy następującą postać równania na przepływ ciepła przez rurę

<ł i

V

^2J[i/vV

które również można napisać w następującej postaci

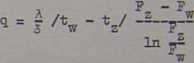
gdzie: F_z, F_w- — zewnętrzną, i wewnętrzna powierzchnia rury.

Oznaczając p _ p z ^{— ł}w 3?

¹¹¹P² w

przez F , otrzymujemy analogiczny wzór do równania Fouriera dla ściany płaskiej z tą różnicą, że tym razem wchodzą-, ca we wzór powierzchnia oznacza w istocie średnią logarytmiczną zewnętrznej i wewnętrznej powierzchni rury

4 | H ^Pm | V    gil

Średnia logarytmiczna jest mniejsza od średniej arytmetycznej , jednak gdy stosunek powierzchni /albo stosunek średnic lub promieni/ rury nie przekracza 2, można prak -tycznie stosować średnią arytmetyczną popełniając błąd mniejszy od 4%. Ze wzoru /13/ wynika, że temperatura ścianki rury zmienia się logarytmicznie. '

2.1.4. Przewodzenie ustalone przez płaską Ściankę wielowarstwowa

Jeżeli ciepło przenosi się przez ścianę złożoną z kilku warstw, to przy ustalonym przepływie ciepła, przez każdą

11