DSC00058 (18)

Zastąpmy E przez ~ i uwzględnijmy prawo Stefana-Boltzman-

<n

na, otrzymany

da

G.T

₁ = ~Jr . dP₁.cosvf₁. dFg.cos^

Odpowiednio powierzchnia aF^ przyjmie z powierzchni dFg energię

6.Tp

dq₂ = ——j . dF^.cos dFg.cos cp^

Pomiędzy povń erzcimi ami zostanie wymieniona energia

/, dF^.costfc₁.dF₀.cos <f₀

,-dq₂ =G/_T;-t£/ -3—|-g    _/56/

ao = aa

gj r

.cos cp^ ,dF₂*cos if₂

757/

Podwójna całka występująca w równaniu /57/ jest funkcją tylko stosunków geometrycznych; nosi ona nazwę współczynnika konfiguracji i jest oznaczana symbolem ₂. Według prawa Steian&-3oltznanna, całkowita energia wypromieniowana przez powierzchnię F,,, padająca w całości na powierzchnię F₂, wy -nosiłaby

^,2 ^sS/T1 “ ^F1    /58/

Stąd widzimy, że współczynnik konfiguracji powierzchni F^ względem powierzchni F₂ wskazywałby jaka część promieniowa -sia powierzchni F^ pada na powierzchnię F_2#

H równaniu /57/ nic się nie zmieni, jeśli przed y.wpiH ęj całki podwójnej postawimy F₂ i do mianownika całki wprowadzimy również Fg zamiast F^. Wtedy

^1,2    " ^'2/ ^2. \\

dF^«cos cp^.dFg.cos <p₂

3T r‘

F.

759/

Całkę występującą w ostatnim równaniu można nazwać współczynnikiem konfiguracji -j powierzchni 3?|. względem 1^. Ostatecznie równania /57/ i /59/ można zapisać w następującej formie

9>i_f2 ®    “ ^T2/ ^P1* ^1,2 |    ip * ^2,1

Stąd wynika

^P1 • ^1,2 ^{= P}2 | ^2,1 ^/6°/

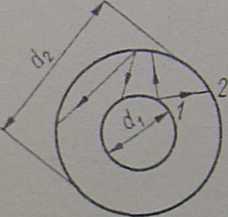
Rys.22. Promieniowanie między rurami.

Ostatnią zależność można wykorzystać do wyznaczenia jednego ze współczynników konfiguracji, gdy znany jest drugi współczynnik. Na przykład jeśli mamy układ, przedstawiony na rys.21, gdy jedna rura jest umieszczona wewnątrz drugiej, wówczas określenie współczynnika konfiguracji dla pro -mieniowania powierzchni rury zew — nętrznej na powierzchnię rury wew -nętrznej jest bardzo trudne,gdyż promienie wychodzące z rury zewnętrznej padają częściowo na powierzchnię wewnętrzną, a częściowo na powierzchnię zewnętrzną. Natomiast wszystkie promienie wychodzące z rury wewnętrznej padają na rurę zewnętrzną, a więc 4^ | | 1. Ponieważ

^P1 * ^1,2 ⁼ P2 * ^2,1

to

‘h * ^1,2 = <*2 * ^ 2 ,1

d, d-

⁹ 2,1 = ^V1,2 ~

Zgodnie z naszymi rozważaniami, współczynniki konfiguracji mogą być obliczone na podstawach czysto geometrycznych.

33