DSC00100 (11)

ZAGADNIENIE TRANSPORTOWE

PnyŁtmd

Durrci jest m dostawców pewnego jednorodnego produktu. Zasoby lego profitu msjó/ifrr się a i-tego dostawcy wynoszą o,(i= 1, 2. .... m). Produkt jest przeznaczony dla m odbiorców, których zapotrzebowanie wynosi adpmtednsj k_h b_;, .... Koszt transportu jednostki produktu od i-tego dotuwey doJ-tegoodbiorcy wynosi e,,(i - /, 2, ... m.J “ /. 2. ...n).

Saiezy określić pian przewozów pomiędzy dostawcami a odbiorcami tak. aby po nwzgięówenm Aultfwydi zasobów dostawców i wymaganego zapotrzebowania odbiorców łączne koszty transportu były minimalne.

traasportowego

*fm3>x,jÓ “ I. Z - m.J- J. 2..... a) amaczł wielkość ptzewozu od i -tego dostawcy doj-iego odbiorcy.

Sfcrarimu zsćzdts można zapisać w następującej postaci:

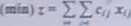
posac Smkcji cdt

wssmki ogMcznau

’ 'wm-imli Włam¹ odhin uiny    J^mMA—»

x„żt i-lJJr— m.

gÓZK X" [r, | macierz zmiennych decyzyjnych (strategia określająca

doił towaru przemieszczanego na drodze (ijjj zeJt wartość funkcji celu (łączne koszty transportu przewozu wszystkich ładunków pomiędzy dostawcami o odbiorcamij C -11> | macierz kosztów (wielkołci ekonomkzno-taryfowe)

« “ I «f | wtłaot óomawy (zasoby dostawców) b^m\b,\ wektorodbioru(zapotrzebowaniaodbiorców)

7-agarimmic transportowe jest szczególnym przypadkiem zadania Piętnowania Urnowego. Postać zadań transportowych pozwala na stosowanie *P«9*Iuycłi metod rozwiązania, charakteryzujących się wysoką efektywnością nawet w przypadku zadań o bardzo dużych wymiarach.

.■<yz    'ha    *0 io jftó-ko

Zadanie transportom; myj nmmj zhUaniewenym jetefi

gladUł&M -

« ^ M_

i«acM» « c»Mr

Warunek len wyraża założoną równość między ofcowitą podażą i cakoweyu

zapotrzebowaniem.

Gdy równość nie jest spefeiiona mówimy, że zadanie jest ninMinwia. Takie zadanie można sprowadzić do zadana zbilansowanego przez wprowadzeń fikcyjnego dostawcy lob fikcyjnego odbiorcy.

1*. Jeśli £a, > ]T k; wprowadzamy fikcyjnego otłaortę z «    X

m    m.

zaponzebowamem b, ** Y a,    - Y k/    oraz przyj n wyr my c_m

M    X

-I    ic*V**>« k r*0^hy^

2* Jeśli ^«| < wprowadzamy fikcyjnego dostawcą z zaptma x    X

pro***“«»“    o»azprzyjn»łe*y    e„-#

^ ^W    ^ art»x<

Większość metod rozwiązywania zadań transportowych jest stosowana do zadań

opisanych modelem zbilansowanym.

•    Zadanie transportowe zbilansowane pojtoifa zawsze co aSjirsgięi rozwiązanie optymalne

•    Każde zadanie transportowe zbilansowane posiada zkaiasmt rozwiązanie optymalne.

f • Z ogólnych wlasnoicl zadania programowania liniowego *ymin ar a rozwiązanie bazowe zadania transportowego tUada jię    z m * a -• i

zmiennych bazowych.

•    IV rozwiązaniu optymalnym zadania transportowego co ncgwyttj m * n - 1 zmiennych jest niezerowych.

•    Jeteh wszystkie e, i bj w zadaniu transportowym zbilansowanym są liczbami całkowitymi, to każde rozwiązanie bazowe (takie optymalne fjest umorzone z liczb całkowitych.

W«S*

WWso-rt

f

i -

!m.«^-r*!. 'oano^ią .    ‘‘-o

■Zu.r*'^,w