DSC00106 (10)

WSISiZ BaltKlaOfłracjijM

PROGRAMOWANIE DYNAMICZNE

Programowanie dynamiczne należy traktować jako sposób podejścia do rozwiązania danego problemu optymalizacyjnego spełniającego dodatkowe warunki.

Podstawowy Warunek, który ogranicza klasę problemów rozwiązywalnych metodą programowania dynamicznego mówi, że N - wymiarowa funkcja celu mus być funkcją separowalną, tzn. można ją wyrazić jako kompozycję N funkcji jednej zmiennej.

Funkcję N zmiennych g    —tu) nazywamy separowalną, Jeżeli

g faj],... ptu) - gi (x,) G>gi (Xi) ©.... e>gr(x_N) gdzie: dwuargumentowy operator kompozycji (B będziemy rozumieć Jako:

•    albo o; tPflj *■ oj + <a>,

•    albo ąi ffiflj - aj *aj,

•    albo ai 8)a) " min (a), ajJ,

•    cdbo O) O a) - max fai, aj).

Istota metody programowania dynamicznego polega na zamianie zadania optymalizacyjnego z N zmiennymi decyzyjnymi w N zadań optymalizacyjnych tylko z jedną zmienną decyzyjną, przy czym zadania te są powiązane zależnością reknrencyjną.

Własność taką posiadają tzw. wieloetapowe procesy decyzyjne.

Proces wieloetapowy deterministyczny (np. realizacja jakiejkolwiek działalności) można podzielić na N etapów.

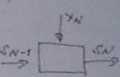
W dowolnym etapie tego procesu można wyróżnić następujące elementy:

1. Stan wejściowy procesu do danego etapu - stan jaki osiągnął proces w

wyniku etapu poprzedniego. Stan ten oznaczamy przez ł*, k - 0,1.....A'-i,

gdzie stan u nazywamy etanem początkowym.

Zmienne stano należą do zbioru stanów dftpnsżczalnyeh j* e Ą.

Z Decyzję podejmowaną na danym etapie. Decyzję opisujemy za pomocą zmktmych ajg fe= 7,2,.... N.

Zmienne decyzyjne na każdym etapie należą do zbioru rozwiązań dopuszczalnych x_feD(.

3. Stan wyjściowy s_t , k -l, 2..... N. procesu zdanego etapu. Stan ten zależy od stanu wejściowego do danego etapu oraz od podjętej decyzji na tym etapie

X4

i i

—A

Schemat wieloetapowego procesu decyzyjnego.

Wieloetapowy proces decyzyjny może być wyrażony następującymi zależnościami rekurencyjnymi:

* = h»(s^{1 2}.i,x_t) (k-l, 2,.... N. s_keS_k, x_teD_t)

Rozwiązanie problemu - określenie ciągu decyzji (wartości zmiennych decyzyjnych) Xi‘, x₂x.i' (x/e Di), przy których ustalona waność funkcji celu dla całości procesu przebiegającego w iV etapach osiągi optimum.

( max) g (xr,Xł... Ah) = gi (x,) tSg₂ (x₂) ©_ <Bg» (x_H)

Ciąg decyzji optymalnych dla kolejnych etapów XI i X₂ i²m( X.v

nazywamy polityką optymalną wieloetapowego procesu decyzyptegp.

Zasada notymalnośd sformułowana przez R.

1

„ Polityka optymalna ma tą własność, ie niezależnie od początkowego stanu s> i pierwszej decyzji Si, pozostałe decyzje muszą stanowit politykę optymalną ze względu na stan wynikający z pierwszej decyzji “

Oznacza to, że jeżeli Xj²,Xj'_t_.» x.v ² jest polityką optymalną dla procesu :V-etapowego, to również polityką optymalnąjest polityka x₂, x_2r~, Xy" dla procesu N-l - etapowego przy stanie początkowym s> - /t/(s®, X/²), wynikającym ze stanu ²« i decyli x/ na pierwszym etapie.

Do najprostszych wieloetapowych procesów decyzyjnych można zaliczyć:

•    problem wyboru najkrótszej drogi,

2

   problem alokacji zasobów,

•    sterowanie zapasami,

•    problem załadunku.