DSC03356 (2)

150

" 8H1P9 podzbiorom formujących nr 1.3-3- olomontu d^ i

ł^d3)¹* ł^ł⁵* {^d10» ^d11> <*12^. [^d2l}^7, ^S}^5, {^d18\⁶> {<J_ą}²,

Crupę podzbiorów formujących nr 1.2.1-1 dla olomontu d^i

Ko)*. Ksi⁵- w,)⁶. i®)⁷

/grupa SPP/

-    8nipę podzbiorów formujących nr 1.2.1.2 dla olomontu d.,-:

K)¹.    KX. <<h₅F. K₇)^b. Ki)⁷

/grupa SWPr/

C^upt podzbiorów formujących nr 1.3*1.1 dla olomontu d_1Q:

^    i ^d15l⁵* i^d17i^6, 1 ^d2o)⁷

/grupa SIPF/

| «^ruPt podzbiorów formujących nr 1.3.1.2 dla olomontu dL_|1*

|gjfe IM²- {*??- Ki)*. K₅l⁵. K₇)⁶- Kil⁷

/grupo SSPP/

—    P^Pt podzbiorów formujących nr 1.3.1 *3 dla olomontu d₁₂^:

i^d,r. i-.)², td?)³. k₂)\ łd₁₅)5,

/frupt 8WPP/

“    podzbiorów formujących or 1.3.2.1 dla olomontu d_1Q:

KV. K)². ) da)³* Kof. ł <l,₅}5, Kef. tc)⁷

/srupo nr/

ff?Pl ^^o4łbloró* formujących or 1.3.2.2 dla olomontu d₁₁s

KF- Kł*. K)³. K,)*, ja^} 5, {d₁₈)⁶. {a^f

/srupo mr/

^Cr°^H podzbiorów formujących or 1.3.2.3 dla olomontu d_l2^l

JM* Kf- KP. W₂f. łd₁₅F. <d₁₈|⁶. i®)⁷

m/

-    grupę podzbiorów formujących nr 1.3-3.1 dla elementu d_1Q»

NS? Ki². W³. Kol*. K₅ł⁵. Keł*. )»)⁷

/grupa BPF/

-    grupę podzbiorów formujących nr 1.3.3.2 dla olomontu d^j

KV- H H Kii*, Ki₅)⁵. k₈i⁶, jjf§

/grupa SWPF/

-    grupę podzbiorów formujących nr 1.3.3.3 dla elementu <L. ,

m¹- ki r§⁵-te^ ssi Bil SI

/grupa BPF/

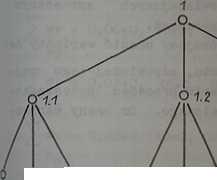
Wygenerowane grupy podzbiorów zaznaczono na drzewie rozwiązań przedstawionym na schemacie 3.43.

13

013.2

L_fd ćTo od doo ooo ptf [m|] |7i^|m2|fu^ jag|taŁ2ltfż? j^łĘgagUar

Schemat 3*^3• Drzewo rozwiązań dla poziomu stanów sąsiednich /p_or. schemat 3.^2/

W wyniku rozszczepienia podzbiorów formujących modelu grafowe-

go uzyskamy 7 dopuszczalnych elementów	przestrzeni	decyzyj-
Mj zgodnych ze stanami sQ( s1f |g	w tabeli	3*2. Są to
kolejno:
d7, d11, d1j, d^, dgą > »	/stan	Są/
<dg» d^# dyf dąi» <L|C« dą7# > »	/stan	n
^<d3* d4# dy, d10, dąj, dą7, dgo > .	/stan	V