DSC07066 (4)

68

Granica funkcji

Asymptoty funkcji • Przykład 2.10

Zamieść asynspiocy pionowe i ukośne podanych funkcji:

=    ^b) s0=) = j~r^:    c) A(x) =

d)p(i)-c-*iaw + r, e) «,(x) - —f) r(_x) = 2^_*.

Hmni|nniB

Fkmkc|a etaraurru mos mieć aaymptoty pionowe jedynie w skończonych Jcrańcach” OK] dziedziny, które do nic] nie należą. Funkcja może mieć nsymptoty ukośne w — co lub w ao tylko wtedy, gdy jej dziedzina jest nieograniczona odpowiednio z dołu lub z góry.

*)    funkcji /(z) = —~ jest zbiór (—cc.O) U (0,oo). Obliczamy zatem granice:

fa,=£-0. UaSH£.,. Km “15 = ,. U„ £=£ =0.

• ¹ *• -    * -O- *    «—O* X    f-w x

Z powyaoego wynika, że prosta y = 0 jest asymptotą poziomą funkcji / w —oo i w co, • P"*** x = 0 nie jest asymptotą pionową tej funkcji (nawet jednostronną).

b| Opędzaną funkcji j<x) = j—— i jest zbiór (—00. l)u(l.oo). Obliczamy zatem granice:

JS. £rri =    (** +^:*•+ 0 - —i

•£?-    T=T ““JS- (**+*+>) = "*

Js- tm~    “ jp®^**+*> =■■*

“ “5.T^r “ JŁl**^+x+1) “ ⁰⁰

Z pawyżnsgn wynika, że prosta x = 1 nie jest asymptotą pionową (nawet jednostronną) amkcp f Ponieważ granice funkcji 9 w obu mcakończonościach są niewłaściwe, więc fcnkcja ta może nart tam ewentualnie aaympcoty ukośne. Współczynnik A_ń asymptoty ‘Anki iJ 9 * A_mx + B_m ohfirzJtmy ze wzoru:

± Bm    k = ± lim    ?— - ±00.

a—w—    x

tam t(ż -1)L

PaoHwM aapółaynmk A, nie jest skończony, więc funkcja fj nie ma saymptot ukośnych

w db* ałsahntW mim di iw.li.

c) Dziedziną    Wż) - - j ^ jest zbiór (-oo,-l) U (—1,1) U (l.oo). Ponieważ

pmijats. więc ■ystsrcjy nlilciyf tylko granica:

1 1

Bca    m —- w —occ

-i* I-i* O*

Bm

I -X¹

» 0.

Z powyższego i z parzystości funkcji h wynika, ie proste z = l ora x = -1 asympto-mmi pionowymi obustronnymi funkcji 6 oraz, ie prosta y = 0 jest jej asymptotą poziomą w obu nieskoóczonaściach.

d) Dziedziną funkcji p(x) = e~' sin X Jest R* Należy zatem obliczyć graniem

lim (e"*sinx + x); lim (e"*iinx + z).

»--w

Pierwsza z tych granic nie istnieje (porównaj Przykład 2.4 f)). natomiast drugn równa de oo, gdyż Um e^-1 sin x = 0 oraz    lim . Oznacza lo, ie funkcja p nie ma asymptoty

i ■

ukośnej w -oo oraz, że może mieć ewentualnie asymptotą ukośną w oo. Współczynniki aaymptoty ukośnej y = A, x -ł* B„ obliczamy ze wzorów;

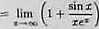
-1;

lim c”'sinx =0.

t—00

= Um ^£1 = Um

D, = lim (p(x) - A+x) = Um^[(e“"zinx+x)-x] =

Zatem prosta y = x jest asymptotą ukośną funkcji p w oo.

e) Dziedziną funkcji q(x) =    jest zbiór |0,4) j(4. oo). Ponieważ punkt z = 0 należy

do dziedziny funkcji, więc asymptotą pionową tej funkcji moio być jedynie prosta i = 4. Obliczamy granice:

oraz

„ x 4 ■ lun _ -- = —— = co.

1-4* y/i—2:

Zatem prosta x = 4 jest asymptotą pionową obustronną funkcji ij.

Przechodzimy teraz do znalezienia nsymptot ukośnych. Ponieważ dziedzina funkcji q jest nieograniczona tylko z góry, więc ewentualna asymptotą ukośna może istnieć tylko w oo. Współczynniki aaymptoty ukośnej y = A+x + B+ obliczamy ze wzorów:

A, = lim

I—M

*ł(«)

Mm

~ o,

= Km (,(*> - A.*) Hm 7^577} f    '“•

Otrzymaliśmy granicę niewłaściwą, zatem funkcja 9 nie ma aaymptoty ukośnej w co.

f) Dziedziną funkcji r(x) = 2 “* jest zbiór (-00,0) U (O.oo). Zatem funteja może mieć nsymptot ę pionową jedynie w punkcie x = 0 oraz nsymptoty ukośne w obu nwskoóczo-nościach. Ponieważ funkcja r jest parzysta, więc badanie wystarczy przeprowadzić na przedziale (O.oo). Obliczamy granico;

lim 2~^ =2“^ ^2-°°=0

órna

Ihn 2 ^ a 2 " =» 2°=* 1.

Z powyższych rozważań wynika, ie funkcja r nie ma aaymptoty pionowej, ma natomiast Mymptoifl poziomą y = I w —co oraz w 00.