DSC07067 (5)

70

Granice funkcji

• Przykład 2.11

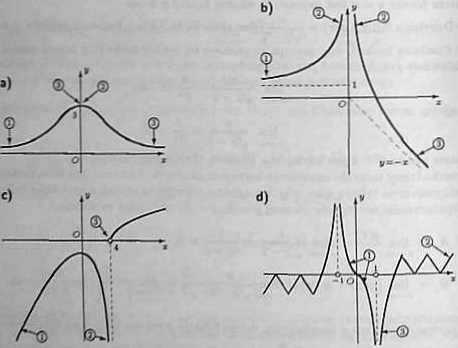
Narysować wykresy funkcji spełniających wszystkie podane warunki:

a)    lim f(x) = 0, lim /(z) = 3, funkcja / jest parzysta;

•' r—-oo    *-.0*    ć j    ••

b)    = 1, liin p(x) = oo, [g(x) +i)»0;

c)    lim h(x} = -oo, lim h(x) = -oo, lim h(x) = 0:

t—«    *—4"    x—4+

d)    funkcja p jest nieparzysta, lim p(x) nie istnieje, lim p(x) = — oo.

X—80    . X—»1

Na rysunkach wskazać fragmenty wykresów spełniające poszczególne warunki. Rozwiązanie

Przykładowe wykresy funkcji spełniających podane warunki przedstawiono na rysunkach. Liczba w kółku oznacza numer kolejnego warunku, który spełnia funkcja.

Zadania

• Zadanie Zl

Korzystając z definicji Heinego granicy właściwej funkcji uzasadnić podane równości:

| lii-2)* - li b) lim (3+2x*) = 5; c) lim - ^ ^z * 0; d) Jlf== —4;

Zadania

e) ljm 8gn(co»i)=i; f) lim £M _{= 1}.

*    *—1+ x. Bafi

• Zadanie 2.2

Korzystając z definicji Heinego granicy niewłaściwej funkcji uzasadnić podane równości:

^c) (z7- QT i    8) “5, (⁵ - *⁷) = -oo.

• Zadanie 2.3

a)    W ostrosłupie trójkątnym prawidłowym krawędź podstaw)* raa długość 6, a kąt nachylenia krawędzi bocznej do podstawy ma miarę x, gdzie 0 < x < —. Niech r(x) oznacza promień kuli wpisanej w ten ostrosłup. Obliczyć granice

lini^ r(x), lim r(x). Czy można podać te granice nie wyznaczając funkcji r?

b)    Cząstka pewnego układu drgającego porusza się po osi Oz. Położenie tej cząstki w chwili Ł > 0 jest opisane wzorem x(t) = 5 — 4"^Sł ęos(2t + 1). Znaleźć jej graniczne położenie, gdy t —► oo. Go oznacza otrzymany wynik?

c)    Równanie ax⁴ -2x—8 = 0 ma dla parametru a > 0 dwa pierwiastki rzeczywiste

Xi(a), X2(a). Obliczyć granice linv xi(a),    Jirn^a:i(ó),

Wskazówka. Narysować wykresy funkcji y = oraz / = 2z + 8. Następnie zbadać położenie punktów wspólnych obu wykresów, gdy a -* 0 oraz, gdy o -f oo.

• Zadanie 2.4

Uzasadnić, że podane granice funkcji nie istnieją:

b) Um£?(x²); d) lim 2™*; f) lim sin^;

x—oo

2fi(*) V}!2o'v''' «vr ^6gnX I

^JUSsgn(x-ł-l)' I) lim \x-E(x)).

a) lim

m x- 3'

c) lim e*cosx;

X—oo

e) lim - - ■*;

• «—2 4 — ar

g) lim ■ x-*ir ąmx

i) Um cos-?;

•*-40-

k) lim e^x(l+8inx);

X —oo