DSC07022 (4)

uczoowe

w

Granice ciągów

• Przykład 1.5

Korzystając z definicji granicy właściwej ciągu uzasadnić podane równości:

a) lim —~ = 2; b) limlog_n+l5 = 0; c) lim 5^=1.

⁹ a-o© n + I    »—OO    ’ M—ób

Rozwiązanie

W rozwiązania wykorzystamy definicję granicy właściwej ciągu (o_n):

JiaZo ⁼°    A V A i(^{n > n}°)⁼* (i°« ~ °i^{< e})b

t>0 n®€N n€N

a) Mamy pokazać, że

A V A I* >"») =» (|stt

c>q n_utH n€fl ’

Niech c będzie dowolną liczbą dodatnią. Musimy znaleźć liczbę no € H taką, że dla każdego n > no spełniona będzie nierówność I-—r —?| < £. Mamy

I 2n l« 4-1

I 2    2

2 -- < e <=> n > 1-

I n + 1    ę

Zatem za n© można przyjąć dowolną liczbę naturalną większą lub równą — - I-Uwaga". Korzystając z funkcji część całkowita Uczbę no można wyrazić wzorem

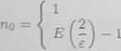
dla e > 1, dla 0<e$ 1.

b) Mamy pokazać, że

A V A jⁿ>    (|^l°gh+i 6 - 0| <«)] •

c>0 HflCH •€!

Niech < będzie dowolną liczbą dodatnią. Musimy znaleźć liczbę no G N taką, żc dla każdego n > n© i pełmona będzie nierówność |log_n+1.S| < e. Marny

L

|k*«*» ^r*| = vi⁵ < € <=» n > 5‘ - li-.

Zat^-m za n© oxóna przyjąć dowolną liczbę naturalną większą lub równą fi • — V. Uwaga*. Korzystając * funkcji część całkowita liczbę n© można wyrazić wzorem

fl© =

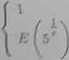
dlą :£ > logy 5,

- 1 dla 0 < c < łog_a 6.

Przykłady

c) Mamy pokazać, że

A V Al(»>"°>=-(I*M<4

«>0 no€H n€W

Niech e będzie dowolną liczbą dodatnią. Musimy znaleźć liczbę no 6 N taką- ** '*'^R każdego « > ⁿo spełniona będzie nierówność | 1/5 — li < Mamy

.... A.,i

jtffi—$j=* Vs-l<e <=* Bⁿ < 1 + c

^ ^n> 1o&(l+0‘

Zatem za no można przyjąć dowolną liczbę naturalną większą lub równą 5Sg_t(ldri) Uwaga*. Korzystając z funkcji część całkowita liczbę no można wyrazić wzorem

l    dlb «> 4,

110 =

fi( !—tW-nI <«» 0 < e $ 4. \log₅(l+c)/

• Przykład 1.6

Korzystając z definicji granicy niewłaściwej ciągu uzasadnić podane równości: a) lim Vn+ 1 = oo; b) lim (n® + n²) = oo; c) lim (5 -2ⁿ) = -oo.

>oo    n—oo    n-*oo

Rozwiązanie

W rozwiązaniach dwóch pierwszych przykładów wykorzystamy definicję granicy mewia śęiwej oo ciągu (d„):

'«n i ą n = do ^ A Ą [(« > "o) =* («» > £)] '

*>o ftoeN neŃ

a w rozwiązaniu trzeciego definicję granicy niewłaściwej -oo:

lim a_n = —co ^ A V A[(^n>n»^{) =>(o}" ^<£)l-

■C<0 n₀tN n€N \

a) Mamy pokazać, że

A V A [(^fl>ⁿ<>ł ==> (+ 1 >£)] •

£>0 n₀€N n€N ^L

S+l>^_n>i

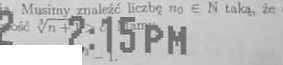
Nieci) £ będzie dowolną liczbą dodą każdego n > no spełniona będzie nieii