DSC07060 (4)

56

Granice funkcji

s) Mmmy pokazać. ws

A    [(ś. *- - °) — (jst - °°)) •

Naecfa (x«) będzie dowolnym magiera spełniającym warunki: x» € .5 (0~) dla każdego n € K. lim x«cO. Wtedy

..    1    _I    1

_v/xT * lim y/x^ O* °°*

Koa^ulany tu z twierdzenia o granicy ilorazu, granicy pierwiastka oraz ze wzoru:

c- sqo dla 0<a(oo.

(T

b) Mamy pnltml, że

A [CS2c*» = -*)=* Csł, ('-*>)—»)] •

!»•>

Niech ;x» I będzie dowolnym ciągiem spełniającym warunek: lim x« w -OO. Wtedy

lim (l -4) = 0W 1 — ^iim x,) *l-(-oo)* = l- «a-».

Ifn ij f ałdnij tu z reguł działali z symbolami nieoznaczonymi.

• Przykład 23

a)    W ostrosłupie czworokątnym prawidłowym krawędź podstawy mu długość p. a wysokość długość z. Niech W(z) oznacza promień kuli opisanej na tym ostro* slupie. Obliczyć granice lim /ł{z), lim /2(x}. Czy można podać te granice nie

x—0+    s oo

wyznaczając funkcji R?

b)    Na prostej położone są ładunki punktowe q i Q. Odległość między nimi jest

zmienna (oznaczamy ją przez r). Wartość siły elektrostatycznej działającej między tymi ładunkami wyraża się wzorem F{r) = |F(r)| =    Obliczyć

granice lim F{r), liro F(r). Podać interpretację fizyczną otrzymanych wyni-

r—O*    »—oo

mm k&w;

c)    Równanie oz³ •*- 3x — 0 = 0 ma dla każdego a > 0 dokładnie jeden pierwiastek peo/ssly x(o). Obliczyć granice lim x(a), lim z(o).

Wskazówka. Narysować wykresy funkcji y = ar³, y «= C - 3x i zbadać położenie punktu wapóioaąoobu wykresów, gdy a —■• O^4- oraz, gdy o —• oo.

ROndąsMlt

jjn Na rysunku przedstawiono przekrój poprzeczny ostrosłupa ABODS płaszczyzną przechodzącą przez wiarzcbolkk ACS. W rozwiązaniu wykorzystamy oznaczenia podane na rysunku. Baeważytny dwa przypadki:

5

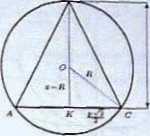
W pierwszym przypadku, stosując twimizaue Pitagorasa do &.KCO, otrzymany

Stad

W drugim przypadku, przeprowadzając podobne obliczenia. otrzymamy ten sam wzór Rw li(*) m | + £ dla 0< x <

lim /?(*) - lim

*—o*    K—o*

lim H(x) = lim

4-»    *—OC

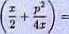
OO.

Wynik ten można uzyskać bez wyznaczania funkcji R. Nioch punkt S porusza się po ■ymetralnej odcinka AC. Wtedy punkt O oddala się nicograniczenic, gdy 5 oddala się nicograniczenic, tzn. R(x) —* oo, gdy z —* oo. Podobnie, jeżeli punkt S zbliża się do K. to punkt O oddala się nieograniczenie. Oznacza to, że R(x) —* oo, gdy z —• (T.

b) Dla funkcji mamy lim /'(r) = oo oraz lim F(r) = 0. W interpretacji fizycznej pierwsza równość

oznacza."żc siła oddziaływania między ładunkami jest dowolnie duża, o ile tylko odległość między nimi jest dostatecznie mała. Natomiast druga równość oznacza, że siła oddziaływania między ładunkami jest dowolnie mała, jeżeli odległość między nimi jest

dostatecznie dużo.

c) Na rysunku przedstawione są wykresy funkcji y = oz^a dla o = ygi« = l.« = W <»■* wykres funkcji y = 6 -3z. Zauważmy, że gdy a— 0*. to wykres funkcji y = oz* ubliża wę- do prostej y - 0. Podobnie, wykres funkcji y * sz* .zbliżę rfę" do prostej *=»0,