DSC07064 (4)

64

Granice funkcji

c) W roawiąianiu wykorzystamy nierówno*! podwójną * - 1 < E{x) $ x dła _x ę R. Żalem dla każdego x > 0 mamy

*- l > *(*) < »

*+i **x+i &«+r

Fimkrje ograniczające spełniają warunki:

lim = 1.    i“» ttt =1-

x + l    *-»!+ 1

Z twierdzenia o trzech funkcjach wynika zatem, ie lim —= 1.

M—CO xtl

d) Dla każdego z > 0 spełnione są nierówności:

xh2    by ^łn(2» + l)^ln(y+y) (x₊i):|_łl2

(x+l)b3 “ b(3*+3*+3*) " b(3* + l) " ln 3=    Jfo3—•

F\inkcje ograniczające spełni a ją warunki:

*»n2    _ ta2    (J + l)ln2 fa-2

•—«o (x+I)In3 ln3*    x—eo    xb3 ln3‘

Z twierdzenia o trzech funkcjach wynika zatem, że

b(y + l) b2 ,

.^.to(F+T) “ to3 '

ę) W rozwiązani u wykorzystamy nierówność

l$£(x)ś2 dla x ę (1,3).

Zatem mamy

(*-*)’ « (*^2)’B(*)g2(*- 2)* dla* E (1,3).

Funkcje (frankujące spełniają warunki:

lm (x - 2)³ = 0,    Um 2(x — 2)³ _S Q,

Z twktdzenia o trzech funkcjach wynika ulem, że

lim (x — 2)^JB(x) = 0.

0 Dla x € B spełnione są nierówności:

r - 1 <E[x) | x. 3* - K E(3x) ^ 3*.

Zatem dla x < 0 zachodzą nierówności

3x E(3x) ^ 3x — 1 x-I * E(x) - x ’

hmkwai frakcje ogranicująrr spełniają warunki:

firn -^*3.

■—-30 X“ 1

Im ^i₌₃

adąe z twierdzenia o trzech funkcjach wynika, ie

Przykłady

65

Twierdzenia o granicach niewłaściwych funkcji

• Przykład 2.8

Korzystając z twierdzenia o dwóch funkcjach uzasadnić podane równości:

a) lim m ■    = oo; b) lim E (= oo; c) Um (2śinx —x) = — oo.

x—O- y/x²-x    r—3" \3-X J    ' *—oo

Rozwiązanie

Rozpoczniemy od przypomnienia twierdzenia o dwóch funkcjach: jeżeli w pewnym sąsiedztwie punktu ze funkcje /, g spełniają nierówność /(z) ( f(z), przy czym funkcja / ma w xq granicę oo, to funkcja g ma w tym punkcie również granicę oo. Podobnie, jeżeli funkcje /. g spełniają w pewnym sąsiedztwie punktu ze nierówność /(z) < $(x), a funkcja g ma w ze granicę -oo. to również funkcja / ma w tym punkcie granicę -oo. Twierdzenie o dwóch funkcjach jest prawdziwe takie dla granic jednostronnych i w nieskończoności, a) Zauważmy, że dla każdego -l < z < O spełniona jest nierówność

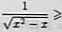
1

Rzeczywiście, jedli z € (—1,0), to podnosząc obie (dodatnie) strony nierówności do kwadratu otrzymamy

z^S:^ -£•

Ostatnia nierówność jest równoważna nierówności

która jest oczywista dla z z przedziału (-1.0). Funkcja ograniczająca z dołu spełnia warunek    8 SBBj

lim . = =    = oo.

»-o- y/-2x    O*

Zatem żądano równość wynika z twierdzenia o dwóch funkcjach.

b) W rozwiązaniu wykorzystamy nierówność E{u) > u - 1 dla u € R. Mamy zatem

Ponieważ

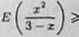
*^a ,_»^a+x-3 3—x    3—x

lim

*-r

x^a-f x —3 3-t

dla 2 < * < 3.

oo,

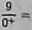
więc i twierdzenia o dwóch funkcjach wynika, że

oo.

c) Dla każdego z € R prawdziwa jat nierówność 2sioz-x £ 2-r. Funkcjo ograniczająca * góry spełnia równość lim (2 — z) = -oo. Z twierdzenia o dwóch funkcjach wynika