DSC07069 (5)

74

Granice funkcji

• Zadanie 2.11

Narysować wykresy funkcji spełniających wszystkie podane warunki:

a)    lim u(x) = oo, lim ti(x) = 1, u(2)i~ 0, Gm u(x) = — 1;

r—-oo    '    0“    •

b)    -jim^ r(i) = e, Gm i/(x) = 0, funkcja v jest parzysta;

c)    prosta y — z + 1 jest asymptotą ukośną funkcji z w -oo, prosta y =* X — | asymptotą ukośną w oo, a prosta x — 0 jest jej asymptotą pionową obustronną;

d)    Gm /(x) = 0, Gm /(x) * 3, lim f(x) = —oo;

*••-00    • *—1    x—*00

e)    Gm s(x) = oo, lim g[x) = -00, lim p(x) = l, lim <j>(x) = 5;

*■" ⁰⁰    • x—oo

f)    Gm h(x) = -4, Gm /»(x) = 00, lim h(x) = 4;

g)    limp(x) = 00, Gm p(x) = 0, funkcja p jest okresowa i ma okres T = 3;

h)    = 4, Gm q(x) = oo, funkcja q jest nieparzysta;

0 _rHjJ_ K¹) = co, jim^ [r(x) - x] = -1, funkcja r jest parzysta.

Na rysunkach wskazać fragmenty wykresów spełniające poszczególne warunki.

Ciągłość funkcji

Przykłady Ciągłość funkcji • Przykład 3.1

Korzystając z definicji Heinego uzasadnić ciągłość podanych funkcji na R a) /(*) = 2x³-3x+5; b) g(z) = c) /i(x) = y/z*+2;    d) p(x) = cosx.

Rozwiązanie

W rozwiązaniach wykorzystamy definicją: funkcja / jest ciągła na R, gdy

A A [(.

MO (*•) ¹ o) Mamy pokazać, że

A ,A .[Cs.—

mci <*.)

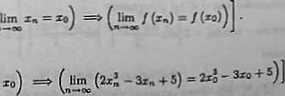
> dowolnym dągfc®

Niech xq będzie dowolną liczbą rzeczywistą orsz niecił (*«) zbieżnym do zo* Wtedy

= 2xl - 3z₀ + 5.

75