72 (206)

6

Przekształcenie Laplace’a

Jedenasty tydzień

Przykłady

mm

Przykład 11.1

Narysować wykres funkcji f(t) i korzystając z definicji wyznaczyć jej transformatę Laplace’a:

0,-(Jj

{0    dla t G (—oo, 0),    (    „

1-e-' dla i G [0,T], b)/(<) = { ^{Sm dla <G} 1 — e~^T dla ł G (T, oo);    l ⁰ poza tym.

Rozwiązanie

a) Wykres funkcji f(t) przedstawiono na rysunku poniżej.

O    x

Korzystając z definicji transformaty Laplace’a mamy

w    a    oo

£{/(<)} ~ J f(t)e-“dt = J (l-e-^,)e-"dt + J (l - e"^T)

0    0    T

TT    oo

= J e~^3t dt- J e-^(>+,)‘ dt+( 1 - t~^T) J e~^a‘ dt

e~^u dt

1

0    T

T    !    .    . i T

=--e -I +

S lo s + 1

S |^p

*T

s s + 1

O--"**)-

1 4* 5

Jedenasty tydzień - przykłady

153

b) Wykres funkcji f(t) przedstawiono na rysunku poniżej.

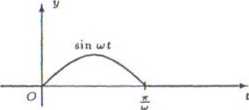
Korzystając z definicji transformaty Laplace’a mamy

OO    _w

dt

£{/(*)} tŁ J f(t)e~“dt = J sinute~³'

s² + w

• (—ssinuit — w cos uii)

3-    /lir \

₀ ⁼ (^e “ + ')

Niech £{/(<)} = F(s). Udowodnić następującą własność przekształcenia Łapiące^

£{/(*- t₀) 1 (t- <₀)} = e~^3t°F(s) dla t₀ > 0.

Rozwiązanie

Mamy

OO

t — tQ - U

dt = du

£{/(t.-t₀)l(t-to)} = [ f (t — to) e^_*‘ di

oo    oo

F(s).

= //(.).-«<-+•.) i...-. J f(u)e~^,u du = e~^3t°

Korzystając z własności przekształcenia Laplace’a wyznaczyć transformaty po-danch funkcji:

a) f(t) — cos² wf; b) /(t) = ch {uit - a) 1 (ud - a); c) /(<) = e^at cos² ud;

■{:

sinud dla t 6 fo, — l a/

poza tym

( 0    dla <6 (-oo,0),

d) /(<)=< l-«“‘ dla < £ [0,T],    e)/(<)

I 1 — e^-T dla i€(T,oo);

Rozwiązanie

.    .    2    1 + cos 2ud

a) Ponieważ cos ud = ---

liniowości przekształcenia Laplace’a mamy

oraz £{cos2ud} =

s² + 4u>²

, więc korzystając z

£ {cos² Ud} = i [£{1(0) + £ {cos2ut}] = \ [i +    j = ₃₍;?₊²;J_a-)