3582319994

METODY ODUCZANIA GRANIC FUNKCJI DWÓCH ZMIENNYCH

I. Obliczanie granic przy wykorzystaniu definicji Heinego granicy funkcji.

Definicja (Heinego)

Niech

(X,d) - przestrzeń metryczna 7 - przestrzeń topologiczna

f \X 7, ge7 ~ element przestrzeni topologicznej P_qe'Dj (F₀ jest punktem skupienia dziedziny funkcji/)

Granicą funkcji/w punkcie P₀ jest element g, lim f(P) = g, wtedy i tylko wtedy, gdy

p->p_a

spełniony jest warunek

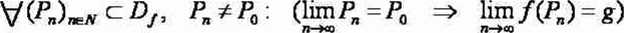
Interpretacja geometryczna

/:R² ->R Po e'Dj

{^Pn)^N - dowolny ciąg, którego wyrazy dążą do P₀ \P_n* P_Q {f{Pn))naN ~ ciąg wartości funkcji/obliczonych w punktach P„P₂,...

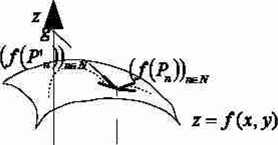
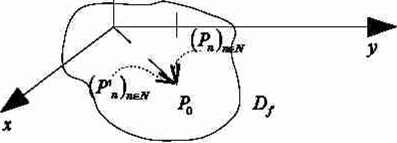
Zamiast rozważać ciągi punktów, rozważmy pewne krzywe (drogi) do których mogą należeć te punkty.

Uwaga

1)    Jeśli dla każdej drogi (krzywej) istnieje granica i jest zawsze ta sama, to funkcja posiada granicę podwójną.

2)    Jeśli dla dwóch różnych dróg otrzymamy różne granice, to funkcja nie posiada granicy podwójnej.

1