DSCN0769

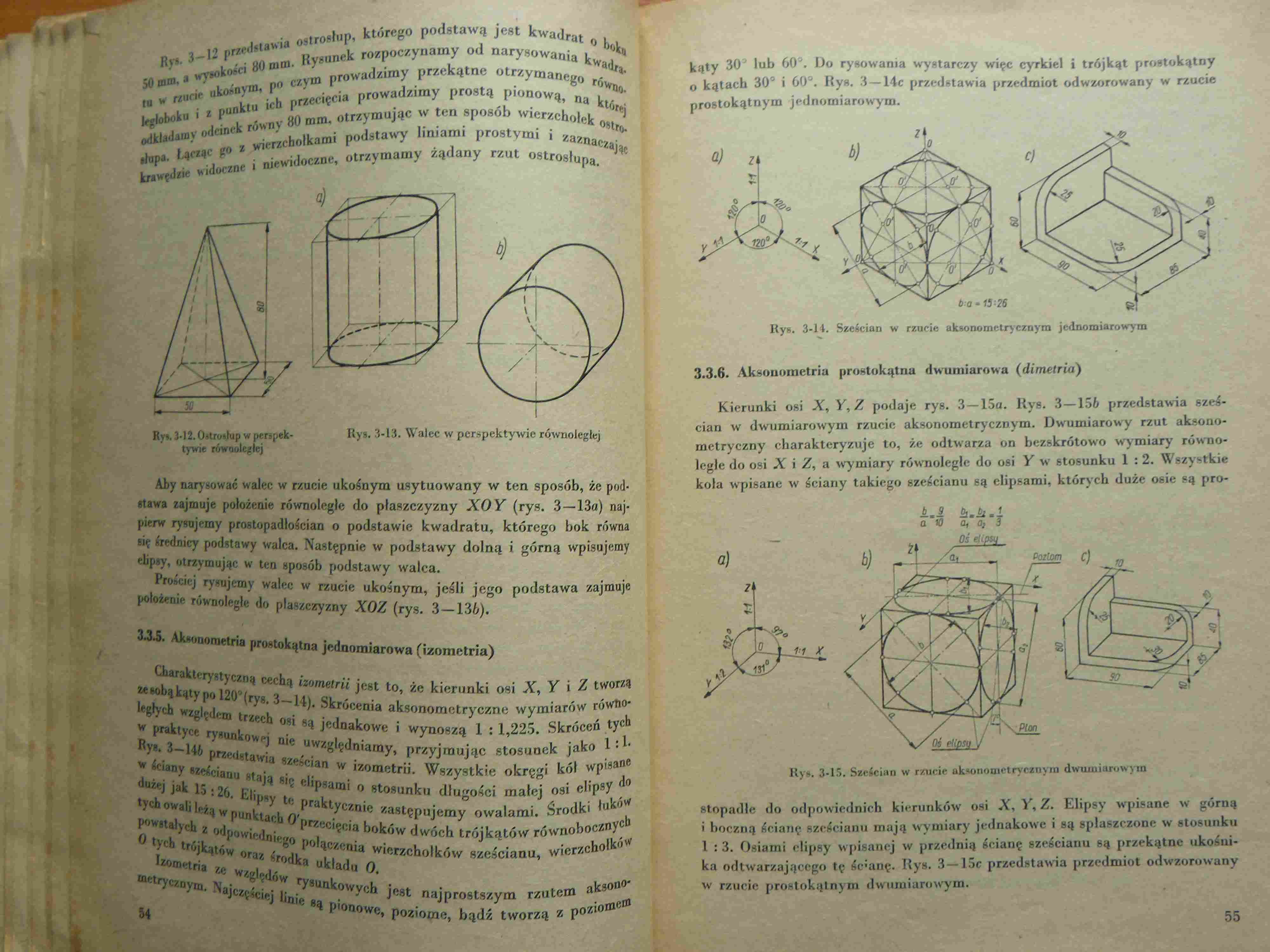
Rys. 3—12 przedstawia ostrosłup, którego podstawą jest kwadrat o foL 50 mm, a wysokości 80 mm. Rysunek rozpoczynamy od narysowania kwadra, tu w rzucie ukośnym, po czym prowadzimy przekątne otrzymanego równo, kgloboku i z punktu ich przecięcia prowadzimy prostą pionową, na której odkładamy odcinek równy 80 mm, otrzymując w ten sposób wierzchołek ostro, słupa. Łącząc go z wierzchołkami podstawy liniami prostymi i zaznaczają krawędzie widoczne i niewidoczne, otrzymamy żądany rzut ostrosłupa.

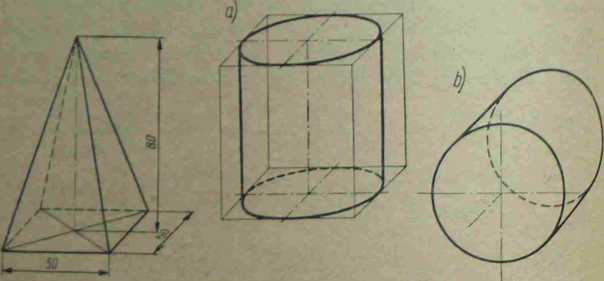
Rył. Ml Ostrosłup w perspek-    Rys. 3-13. Walec w perspektywie równoległej

tywie równoległej

Aby narysować walec w rzucie ukośnym usytuowany w ten sposób, że pod* stawa zajmuje położenie równoległe do płaszczyzny XOY (rys. 3—13o) najpierw rysujemy prostopadłościan o podstawie kwadratu, którego bok równa się średnicy podstawy walca. Następnie w podstawy dolną i górną wpisujemy elipsy, otrzymując w ten sposób podstawy walca.

Prościej rysujemy walec w rzucie ukośnym, jeśli jego podstawa zajmuje położenie równolegle do płaszczyzny XOZ (rys. 3—136).

3.3.5. Aksonornetria prostokątna jednomiarowa (izometria)

Charakterystyczną cechą izometrii jest to, że kierunki osi X, Y i Z tworzą ze sobą kąty po 120° (rys. 3—14). Skrócenia aksonomctryczne wymiarów równoległych względem trzech osi są jednakowe i wynoszą 1 :1,225. Skróceń tych w praktyce rysunkowej nie uwzględniamy, przyjmując stosunek jako 1:1. Rys. 3—146 przedstawia sześcian w izometrii. Wszystkie okręgi kół wpisane w ściany sześcianu stają się elipsami o stosunku długości małej osi elipsy do dużej jak 15 :26. Elipsy te praktycznie zastępujemy owalami. Środki luków tych owali leżą w punktach 0'przecięcia boków dwóch trójkątów równobocznych powstałych z odpowiedniego połączenia wierzchołków sześcianu, wierzchołków O tych trójkątów oraz środka układu O.

Izometria ze względów rysunkowych jest najprostszym rzutem aksono-metrycznym. Najczęściej linie są pionowe, poziome, bądź tworzą z poziomem

kąty 30’ lub 60°. Do rysowania wystarczy więc cyrkiel i trójkąt prostokątny o kątach 30° i 60°. Rys, 3—14c przedstawia przedmiot odwzorowany w rzucie prostokątnym j ednomiarowym.

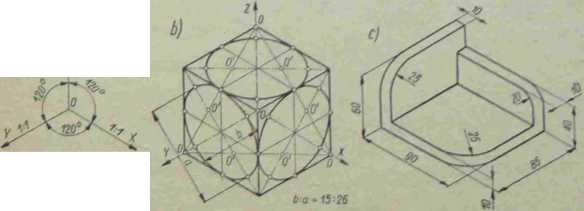
Rys. 3-14. Sześcian w rencie aksonometrycznym jedno miaro wym

3.3.6. Aksonometria prostokątna dwumiarowa (dimetria)

Kierunki osi X, Y, Z podaje rys. 3—lSa. Rys. 3—156 przedstawia sześcian w dwumiarowym rzucie aksonometrycznym. Dwumiarowy rzut aksóno-metryczny charakteryzuje to, że odtwarza on bezskrótowo wymiary równoległe do osi X i Z, a wymiary równolegle do osi Y w stosunku 1 :2. Wszystkie kola wpisane w ściany takiego sześcianu są elipsami, których duże osie są pro-

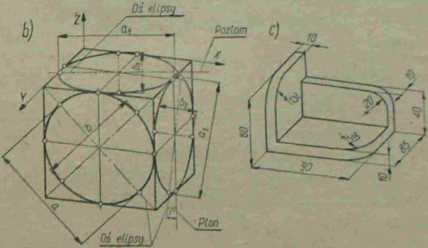
Rys. 3-15. Sześcian w rzucie aksonometrycznym dwumiarowym

stopadłe do odpowiednich kierunków osi X, Y, Z. Elipsy wpisane w górną i boczną ścianę sześcianu mają wymiary jednakowe i są spłaszczone w stosunku 1 :3. Osiami elipsy wpisanej w przednią ścianę sześcianu są przekątne ukośnika odtwarzającego tę śc*anę. Rys. 3—15c przedstawia przedmiot odwzorowany w rzucie prostokątnym dwumiarowym.

55