DSCF6552

60

3. Pomiary

Proces przejścia kulki przez rzędy prętów odpowiada pojedynczemu pomiarowi; każde zderzenie z prętem markuje błąd elementarny, a położenie przegródki, do której ostatecznie wpada kulka, odpowiada wynikowi pomiaru. Wartość dokładną wielkości mierzonej symbolizuje położenie szczeliny przez którą wrzucane są kulki. W wypadku, gdy szanse odchylenia kulki w zderzeniu z prętem w lewo lub w prawo są jednakowe, największe jest prawdopodobieństwo trafienia kulki do przegrody środkowej, położonej pod szczeliną.

W praktyce nie wyrzuca się wielokrotnie jednej kulki, lecz jednokrotnie kilkaset jednakowych. W przegródce środkowej będzie wówczas prawdopodobnie więcej kulek niż w którejkolwiek z pozostałych. Jeśli jednak prawdopodobieństwa odchylenia kulki w lewo lub w prawo nie są jednakowe (można to zrealizować wprowadzając ukośną szczelinę wlotową), wówczas maksymalna liczba kulek trafi do przegródki przesuniętej względem środka Przesunięcie takie odpowiada w naszej analogii pojawieniu się błędu systematycznego. Niepożądane przesunięcie pojawi się również w przypadku niewłaściwego ustawienia tablicy.

Funkcja wiążąca ilość kulek w przegródce z odległością tej przegródki od środka tablicy dąży do gęstości rozkładu normalnego w wypadku, gdy wzrasta liczba poziomych rzędów prętów, a maleją średnice kulek, odległości między prętami i szerokość przegródek.

4. Zastosowanie

Wymieńmy tylko dwa przykłady ilustrujące znaczenie rozkładu normalnego:

-    wyjaśnienie mechanizmu ruchów Browna (Smoluchowski i niezależnie Einstein, 1905-1906);

-    zastosowanie rozkładu normalnego w rachunku błędu i statystyce.

S. Pomiary i opracowanie

Wykonanie ćwiczenia ogranicza się do wrzucenia kilkuset kulek (optymalna liczba kulek jest równa kwadratowi liczby przegródek) i policzeniu kulek w każdej przegródce. Kulki należy wrzucać pojedynczo, co w naszej analogii odpowiada niezależności pomiarów.

Przy opracowywaniu ćwiczenia można opierać się na przykładzie 5.3.2. a także na opisie tablicy Galtona w [7].

Pytania

1.    Jak wpływa liczba poziomych rzędów w tablicy Gal tona na dyspersję otrzymanego rozkładu?

2.    Opisać urządzenie mogące być mechanicznym „generatorem” rozkładu prostokątnego.

ST-2. Eksperyment statystyczny z użyciem wagi automatycznej [9]

1. Wstęp

Opisane tutaj ćwiczenie polega na dokonaniu oceny parametrów dwu populacji (populacji monet z dwu różnych lat emisji) w oparciu o badanie niewielkich próbek.

Po otrzymaniu rozkładów mas monet należy ustalić, czy wartości średnie obu próbek różnią się w sposób istotny, tzn. czy próbki pochodzą prawdopodobnie z różnych populacji.

Wielkościami mierzonymi są masy monet określonego nominału, podzielonych na dwie grupy w zależności od roku emisji. Wartość średnią masy w każdej grupie oraz średni błąd kwadratowy pojedynczego pomiaru i średniej próbki znajdujemy ze znanych wzorów:

lii!    i

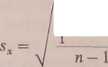
(2)

ifL

■jn

(3)

gdzie n oznacza liczbę monet w próbce.

Aby odpowiedzieć na pytanie, czy wartości średnie obu próbek różnią się w sposób znaczący, opisujemy otrzymane rozkłady za pomocą funkcji