DSCF6563

82

2. Zasada pomiaru

Pomiar oparty jest o wykorzystanie własności drgań skrętnych.

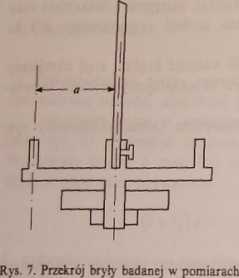
Moment sił sprężystości pojawia się przy obrocie wahadła o kąt tp:

N = — D(p    (2)

gdzie D oznacza tzw. moment kierujący.

Po wykorzystaniu związku N = Itp (N oznacza moment siły) otrzymamy równanie ruchu:

(p + ~ę = 0    (3)

Jest to równanie ruchu harmonicznego:

gdzie:

ę + (o²q> = 0

(4)

(5)

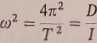
Ze wzoru 5 otrzymujemy wyrażenie na okres wahań:

^{T = 2n}Jl    ⁽⁶⁾

Ponieważ nie znamy ani momentu bezwładności I, ani momentu kierującego D, konieczne jest dołączenie jeszcze jednego równania. Stanowi je wyrażenie na okres drgań wahadła obciążonego dodatkowymi bryłami foremnymi, których moment bezwładności można łatwo policzyć:

T_t

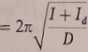
(7)

Układ równań 6 i 7 można rozwiązać względem I:

l =

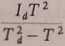
(8)

Dodatkowe bryły użyte w ćwiczeniu mają kształt wydrążonych walców, o promieniu zewnętrznym r₂ i wewnętrznym r₂. Moment bezwładności takiej bryły wyraża się wzorem:

§§!§§ 1

gdzie m oznacza masę walca.

Wpływ każdego walca na moment bezwładności całego układu będzie zależny od odległości walca od osi obrotu układu a. Zgodnie z zasadą Steinera:

I_a = l_w + ma²    (10)

3. Pomiary i opracowanie

Po kilkakrotnym dokonaniu niezbędnych pomiarów pomocniczych (r_lt r₂, a, m) znajdujemy średnie wartości mierzonych wielkości i odpowiednie niepewności. Pozwoli to obliczyć, opierając się na wzorach 9 i 10, moment bezwładności /, każdego z czterech krążków oraz znaleźć całkowity dodatkowy

moment bezwładności I_d = £ J, oraz niepewność

i=i

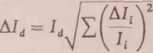
gdzie Al, oznacza niepewność pomiaru momentu bezwładności i-tego walca. Po zmierzeniu czasu np. 20 drgań skrętnych wahadła nieobciążonego, a następnie obciążonego czterema wydrążonymi walcami, znajdujemy okresy T i T_t oraz niepewności AT i AT_d.

Następnie na podstawie wzoru 8 znajdujemy moment bezwładności bryły nieregularnej I. Niepewność Al można ocenić ze wzoru:

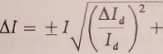
2T²AT j² T(T^ad - T²)

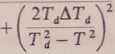
Pytania

1.    Uzasadnić związek 9.

2.    Przypuśćmy, że dodatkowe walce mogą obracać się bez tarcia wokół swoich osi. Jak zmieni się wówczas okres drgań wahadła?