DSCF6575

106

2a. Fale stojące — ujęcie matematyczne

Doskonale giętka i sprężysta struna, napięta w stanic równowagi siłą F₀ znajduje się w ośrodku, który nie stawia oporu jej drganiom. Jeżeli spowodujemy krótkotrwałe, bardzo małe odchylenie fragmentu tej struny od stanu równowagi, to składowa F_y siły wypadkowej, dążącej do przywrócenia stanu równowagi będzie równa (zgodnie z oznaczeniami i orientacją osi, przyjętymi na rys. 21):

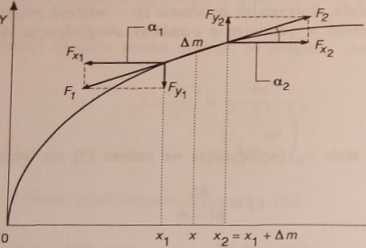
Rys. 21.

X

F_y = F₂ sin H — Fj sin a,    (1)

Jeżeli wychylenie z położenia równowagi jest niewielkie, wówczas możemy przyjąć, iż F_t as F₂ as F₀ oraz sin a_Ł as tg aj i sin a₂ as tg a₂, co pociąga za sobą

^Fi = ^fo(tg “z-tg “x)    (2)

Ponieważ a_t i a₂ są kątami nachylenia stycznych w punktach (x_lt yj i (x₂, y₂) do struny względem osi OX, to

tg aj

n

1 tg ^a2

\dxjlx₂.y₂)

(3)

W związkach tych celowo użyto symboli pochodnych cząstkowych, gdyż wychylenie struny z położenia równowagi jest funkcją nie tylko współrzędnej x ale i czasu t: y = y(x, t).

podstawiając (3) do (2) otrzymamy

n	(^dA
\^SxJ U2.y2)	\5-X/(X|.,1)|

FMx + Ax, t ~/(x, t)]

(4)

Rozwijając funkcję zawartą w nawiasie kwadratowym w szereg Taylora i odrzucając wyrażenia wyższych rzędów (zgodnie z przyjętym założeni® bardzo małych odchyleń od stanu równowagi) dochodzimy do zależ-aości:

_F =_F ^d2y(^x>Q

m ⁰ dx²

Ax

(5)

W momencie zaniku sił powodujących wychylenie z położenia równowagi tlement struny zacznie się poruszać z przyspieszeniem o składowej pionowej

Wk

1it¹

i zgodnie z II zasadą dynamiki

(6)

_{n r} d²y(x,t)    d²y(x,t)

gdzie Am = p,Ax jest masą elementu zaś p, - masą jednostki długości juuny, czyli tzw. gęstością liniową. Otrzymujemy stąd równanie dla fal poprzecznych w strunie

d²y(x,t) _ F₀ d²y(x, t)    _

dt² p, dx²

w którym to równaniu wielkość F/p, jest równa kwadratowi prędkości fali.

A zatem

HR! RIH    /o\

_—| i

&

V Pi

Ograniczmy nasze rozważania do fal będących drganiami harmonicznymi. | takim przypadku jedna z funkcji spełniających równanie (7) powinna być funkcją postaci