dupa0036

jaj (.Vj). Średni poziom tak podanej zmiennej można obliczać jedynie za pomocą średniej harmonicznej, zgodnie ze wzorem (2.22):

■*// =

10000

5

30000

10000 10000 +-+-

= 4,865 szt/10000 zl

Otrzymana wielkość oznacza, że za 10 tys. można kupić średnio 4.865 jajka, a zatem średnia cena jednego jajka jest odw rotnością tej wielkości:

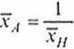
10000

4,865

= 2056 zl/szt

Średnią cenę jaj można oczywiście obliczyć, posługując się średnią arytmetyczną (2.14), jednakże wymaga to wcześniejszych przekształceń informacji wyjściowych tak, aby ustalić cenę jednego jajka w badanych sklepach.

I    sklep: 10000 zl: 5 szt = 2000 zl/szt - x\\

II    sklep: 10000 zl: 4 szt = 2500 zl/szt -

III    sklep: 10000 zl: 6 szt = 1667 zl/szt - .r₃;

X_A- [2000 + 2500 + 1667) : 3 = 2056 zl/szt.

Średnia geometryczna

Średnia geometryczna jest pierwiastkiem w-tego stopnia z iloczynu wszystkich wartości badanej zmiennej, przy czy wartości cechy muszą być większe od zera.

(2.23)

Wr-v„

W literaturze statystycznej¹ można spotkać się ze stwierdzeniem, że średnia ta ma jedynie sens wtedy, gdy badana zmienna jest multiplikatywna, a zatem w logiczny sposób wartości jej mogą być przez siebie mnożone, a otrzymany iloraz może zostać rozdzielony równomiernie na wszystkie obserwacje. Warunek ten spełniają pewne charakterystyki liczbowe, opisujące zmiany zjawisk w czasie (będzie o tym mowa w rozdz. 4), stąd też średnia ta jest

stosowana głównie w analizie szeregów czasowych, jako miara średniego przerostu.

Na podstawie danych o wolnorynkowym kursie dolara (Biuletyn Statystyczny GUS 1994, nr 1. s. 21) obliczono, że w 1 kwartale 1993 r. cena dolara wzrosła o 6.7%, w II kwartale o 3,1%, w III kwartale o 12,9%, a w IV o 7,4%. Chcąc ustalić, o ile średnio zwiększa! się z kwartału na kwartał kurs dolara, posłużymy się średnią geometryczną, ponieważ ocena podziału zaobserwowanych wartości zmiennej pomiędzy cztery kwartały wymaga, aby wartości te zostały przez siebie przemnożone. (Obliczenia są prostsze, gdy wykonujemy je na ułamkach niż na . procentach).

x_(! =    067-1,031-1,129-1,074 = iftf339 = 1,075

A zatem w 1993 r. z kwartału na kwartał dolar drożał średnio o 7,5%. Otrzymany wynik mieści się w przedziale 3,1% < x_G <12,9%.

Średnia geometryczna bywa również stosowana wtedy, gdy cecha nic ma charakteru multiplikatywnego, czyli jest wyrażona w liczbach absolutnych, ale w zbiorze informacji występują wartości skrajne, różniące się znacząco od większości zaobserwowanych wartości cechy. W takich wypadkach średnia geometryczna lepiej niweluje wpływ tychże wartości skrajnych na ocenę średniego poziomu, jest ona mniej wrażliwa na ich działanie aniżeli średnia arytmetyczna.

1*2.9. Dokonano pięciu pomiarów głębokości pewnego jeziora, otrzymując następujące informacje [w metrach): 2; 2,5; 2; 1,5; 14. Na tej podstawie należy ocenić średnią głębokość jeziora.

Obliczając średnią arytmetyczną, otrzymujemy:

X_A= (2 + 2,5 + 2 + 1,5 + 14): 5 = 4,4 m

Obliczaj.ąc średnią geometryczną, otrzymujemy:

,v_G = V2-2.5-2-l.5-14 = tfm =2,91 m

Widzimy, że zastosowanie średniej geometrycznej dało wy nik bardziej zbliżony do tych wartości cechy, przy których występowało skupienie obserwacji.

67

1

l^>or. D. Szulc, Statystyka dla ekonomistów, t. 1, Warszawa, PWH 1967, s. 171. 66