Egzamin6

Egzamin z malenia! vki dyskretni j i Ki I li - 1’rzykl id :

Q Rozwia/ać równanie rekurencyjne: a,, — dr}<?_h-i — -f-o dla fi > 0 i ao ~ k

1. He poehodnyeh cząstkowych funkcji f : R" —* R w U rzydu 2!) tnożi a polirzyc przy założeniu, że funkcja jest klasy (( czyli pochodne mieszane sa rdycne)?

Xa ]>alu jest u par małżeńskich, n paniom losowo wybierany partnera do tańca sposrod n panów (każdej innego)- -Jakie jest prawdopodobieństwo, że o,dna para małżeńska nie bodzie w tym tańcu tańczyć razem?

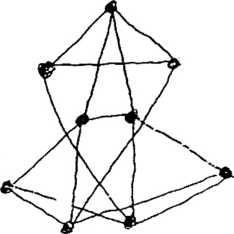
(§) Czy dany .uraf (i jest eulerowski. hamiltonowski. dwudzielne*

Wv7naizvVy^((!) oraz y(G) dla. danego grafu G.    (C *

(£k) 1 le jes- grafów izomorficznych z danym grafem T i równych o<| niego.

A

-4

Za

każde zadanie można uzyskać mal-symal tie 10 piiriktow.

Egzamin z matematyki dyskretnej {Eii !) Przykk d J

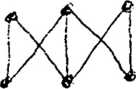
Q ('z\ dam raf G jest eulerowski. hamiltonowski. dwudzielny?

a równanie

© Ile rozwiazari w liczbach całkowi ty cli łiieujemiiych. nieparzystych i poilzieinwh przez d m

~h X i Xa — lb8

Rozwiązać równanie rekurencyjne: h_n = Rnb,,-\ — 10/* -ł- l dla u > 0 i V = d.

ÓJ	u enkterk	o w m;
	j»rzez. <i*».	■.ollie
	• lzic« k« * i>	t rzym
©	Ile |est g!	afów

Za każde zadanie można uzyskać mal-symal de i() puhklow.