fizyka019

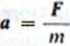
Układy odniesienia, o którym mówi I zasada dynamiki, noszą nazwę układów inercjalnych. O innych układach, tzw. nieinercjalnych, będzie mowa w paragrafie 8.

Dla ilustracji pojęcia układu inercjalnego rozważmy przypadek dwóch układów odniesienia i dwóch obserwatorów, z których jeden — obserwator A — znajduje się w układzie Oxyz związanym z peronem, drugi zaś — obserwator A' - znajduje się w układzie 0'x'y'z' związanym z wagonem jadącym ze stałą prędkością u po torzc prostym (rys. 5-1). W wagonie na idealnie gładkiej podłodze znajduje się ciało o masie m, przy czym siły grawitacji i reakcji podłoża działające na to ciało równoważą się. Jak opisze zachowanie się ciała każdy z obserwatorów?

y I zasada i . dynam! " 4
	{	^y (i nasada i J dynam^1/^1	V
	& W
0	X

K>». 5-1

Obserwator A' stwierdzi, żc w jego układzie O'x'y'z ciało zachowuje stan spoczynku, ponieważ nic działa nań żadna siła wypadkowa.

Obserwator A stwierdzi, że na ciało nic działa żadna siła wypadkowa i dlatego porusza się ono ze stałą prędkością v po torzc prostym?

Obaj obserwatorzy stwierdzili zgodność zachowania się ciała z pierwszą zasadą dynamiki. Zatem oba układy odniesienia: Oxyz oraz 0'x'y'z' są układami inercjalnymi.

II zasada dynamiki: Jeżeli na ciało o masie ni działają siły niezrównoważone o wypadkowej F, to ciało porusza się ruchem przyspieszonym z przyspieszeniem a takim, żc (5.1)

W zadaniach dynamiki to równanie ruchu będziemy zapisywać najczęściej w postaci wektorowej

F = ma    (5.2)

lub za pomocą składowych

F_x = ma_x, F_y = ma_r F_z = ma_t

gdzie wskaźnikami x, y, z oznaczono składowe wektorów względem odpowiednich osi układu współrzędnych.

Jeżeli siła F = const, to ruch jest jednostajnie zmienny. W zadaniach lego paragrafu będziemy rozważali tylko takie przypadki.

Obydwie zasady mówią o jednym ciele, jednakże w' zadaniach dynamiki zawsze będziemy mieli do czynienia z układami co najmniej dw'óch ciał działających nawzajem na siebie i wtedy stosujemy III zasadę dynamiki, licz dokładnego zrozumienia której nic sposób rozwiązać najprostszych nawet zadań.

III zasada dynamiki: Jeżeli ciało A działa na ciało B siłą F„, to ciało // oddziałuje na ciało A taką samą co do wartości siłą F_A, lecz skierowaną przeciwnie. Siły te są jednakowe co do wartości i skierowane przeciwnie, lecz nic znoszą się ani nie równoważą, gdyż są przyłożone do różnych ciał.

Przy rozwiązywaniu zadań z dynamiki należy zwrócić uwagę na kolejność czynności, charakterystyczną dla tych zadań, mianowicie:

1)    wykonujemy rysunek, wyraźnie zaznaczając odrębność ciał tworzących układ:

2)    badamy, jakie siły działają na poszczególne ciała tworzące układ i rysujemy te siły;

3)    przyjmujemy układ odniesienia, w którym będziemy zapisywać równania ruchu: wybór kierunków osi układu zależy od treści zadania, przy czym należy obrać je tak, by równania ruchu miały jak najprostszą postać:

4)    zapisujemy dla każdego ciała osobno równanie II zasady dynamiki.

Dla ilustracji zbadajmy przypadek, gdy skrzynia o masie m leży na szal-

cc wagi sprężynowej i narysujmy (rys. 5-2) siły działające na ciała: skrzynię ■I i wagę B. Rysujemy schematycznie skrzynię (nazwijmy ją ciałem A) na wadze sprężynowej (ciało B). Aby podkreślić, żc w tym zadaniu traktujemy skrzynię A i wagę B jako dwa odrębne ciała. rysujemy je jak na rys. 5-2b, a nic jak na rys. 5-2a. Zaznaczając wyraźnie odrębność tych ciał unikniemy w ten sposób wielu nieporozumień.

Następnie badamy, jakie siły działają na ciała i gdzie są one przyłożone:

— w środku masy ciała A jest przyłożona siła ciężkości mg: rysujemy tę siłę,

43