fizyka026

5-39R. Na ciało o masie m działa siła stale w kierunku ruchu ciała. Siła ta zmienia się jednostajnie od wartości zerowej do F w czasie /. Oblicz prędkość i>₀, z jaką ciało rozpoczęło ruch, jeżeli siła działająca zwiększyła prędkość ciała dwukrotnie.

6. Dynamika ruchu punktu materialnego po okręgu

W zadaniach tego paragrafu są omawiane tylko te przypadki, gdy punkt materialny porusza się po okręgu (po torze kołowym) ze stałą prędkością kątową m. Wówczas prędkość liniowa punktu poruszającego się po okręgu pozostaje stała co do wartości ]r| = const. Podobnie przyspieszenie dośrodkowe, choć zmienne co do kierunku, zachowuje też stałą wartość |aj = = const.

Z paragrafu 4 wiemy, że wartość przyspieszenia dośrodkowego może być obliczona z poniższych wyrażeń

lub a_d = io²R

(6.1)

gdzie R — promień okręgu, po którym porusza się punkt materialny.

Zgodnie z II zasadą dynamiki, ruch z przyspieszeniem może odbywać się tylko wtedy, gdy na ciało działa niezrównoważona siła, pochodząca od innych ciał. W przypadku ruchu po okręgu zachodzącego ze stałą prędkością kątową siła ta jest stała co do wartości i stale skierowana prostopadle do wektora prędkości (rys. 6-1). Zmienia ona więc jedynie kierunek prędkości. Siła ta, nazywana silą dośrodkową F_d, nadaje ciału przyspieszenie dośrodkowe, a więc

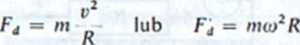
(6.2)

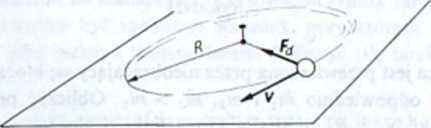
Rys. 6-1

W zadaniach na ogół nie korzystamy z zapisu wektorowego, a posługujemy się tylko wartościami siły i przyspieszenia dośrodkowego, pamiętając, Ac siła ta jest skierowana do środka toru. W zapisie wektorowym równania (6-2) mają postać

- mcj²R

R

R

lub

— m

v² R R R

gdzie

R

R

jest wektorem jednostkowym

skierowanym od środka toru na

zewnątrz.

Ponieważ w ogólnym przypadku siła F_d może być wypadkową wielu sił działających równocześnie ma masę m, więc przystępując do rozwiązywania jakiegokolwiek zadania z dynamiki ruchu po okręgu, zawsze zaczynamy od przeprowadzenia analizy sił działających na poruszającą się po okręgu masę m. Kolejność postępowania jest następująca:

1)    wykonujemy rysunek,

2)    badamy, jakie siły działają na masę m,

3)    rysujemy te siły, wyraźnie zaznaczając, która siła na co działa,

4)    znajdujemy siłę wypadkową lub siłę składową, która działa na masę m w kierunku do środka toru; ta wypadkowa lub składowa siła jest siłą dośrodkową F_d,

5)    zapisujemy równanie ruchu II zasady dynamiki podstawiając na miejsce przyspieszenia a wartość przyspieszenia dośrodkowego a_d ze wzoru (6.1). W ten sposób wybieramy układ współrzędnych, w którym oś jest skierowana do środka okręgu.

Powyższe uwagi zilustrujemy na przykładzie. Niech ciało o masie m, uwiązane na nici o długości R, porusza się po okręgu w płaszczyźnie pionowej (rys. 6-2a). W najwyższym punkcie toru na ciało działają dwie siły: siła ciężkości mg oraz siła T, przyłożona od strony nici (równa napięciu nici). Wypadkowa tych sił jest skierowana do środka toru; jest ona równa sile dośrodkowej F_d. Na podstawie wzoru (6.2) piszemy

v²

mg + Tt = m ^

Stąd możemy obliczyć wartości siły 7",, jaką sama nić działa na ciało, mianowicie

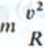
— mg

57