freakpp029

56

3.3. Wyznaczanie dyfuzyjności cieplnej metodą chłodzenia kuli

3.3.1 Stanowisko pomiarowe

Do wyznaczenia dyfuzyjności cieplnej danego materiału metodą stanu uporządkowanego wykonuje się kulę z tego materiału. Dokładnie w jej środku umieszcza się termoelement do pomiaru temperatury.

Schemat stanowiska pomiarowego przedstawiono na rys. 3.6.

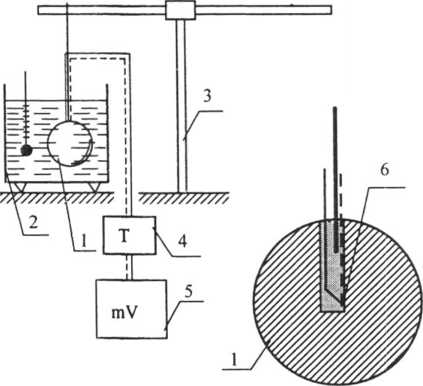
1.    Badane ciało

2.    Ultratermostat

3.    Statyw

4.    Termostat

5.    Miliwoltomierz

6.    Termoelement

Rys. 3.6. Schemat stanowiska pomiarowego

3.3.2. Wykonanie pomiaru

Kulę z danego materiału, zawieszoną na statywie, umieszcza się w ultrater-mostacie. Następnie kulę nagrzewa się do zadanej w ultratermostacie temperatury, wyższej od temperatury otoczenia. Czas nagrzewania musi być tak długi, aż uzyska się stałą temperaturę w środku kuli, co należy sprawdzić na mierniku temperatury. Po nagrzaniu kuli i ustaleniu się temperatury wyjmuje się ją z termostatu i zawiesza swobodnie na statywie, aby mogła chłodzić się w powietrzu. Od chwili umieszczenia kuli w powietrzu odczytuje się wskazania miernika temperatury w równych odstępach czasu, np. co pół minuty. Odczytane wartości oraz obliczone inne potrzebne wielkości jest wygodnie umieścić w tabeli (patrz tab. 3.2).

Tabela 3.2. Zestawienie wyników pomiarów

t	T		0	In0
s	mV	°C	-	-

3.3.3. Opracowanie wyników

Obliczenie dyfuzyjności cieplnej odbywa się na podstawie wzoru (3.29). Biorąc pod uwagę pierwszy wyraz szeregu, otrzy muje się:

O = Cexp

2 at

(3.35)

Po zlogarytmowaniu, dla dwu różnych chwil czasowych, jest:

lnO|

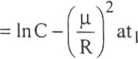
ln©₂

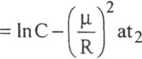
(3.36)

Dwie chwile czasowe: tj i t2 wybiera się na prostoliniowej części wykresu rozkładu temperatury w czasie, przedstawionego na rys. 3.1, który uzyskuje się na podstawie wyników pomiaru. Ze wzoru (3.36) można obliczyć a:

(3.37)

V lnOj - ln©2 kPy ^t2~^t\

Stałą |l, występującą we wzorze (3.36), wyznacza się następująco. Zgodnie ze wzorem (3.30) stała C jest powiązana funkcją uwikłaną ze stałą ji. Stałą C, dla stanu uporządkowanego, wyznacza się, przedłużając prostoliniową część wykresu, na rys. 3.1, do przecięcia się z osią pionową, otrzymując tym samym wartość -ln©₀. Z równania prostej

ln©₀ = ln0₂ + (ln©] - ln©₂)

*2

t₂ -tj

(3.38)