f = (x4,x3,x2,x1) wariant I
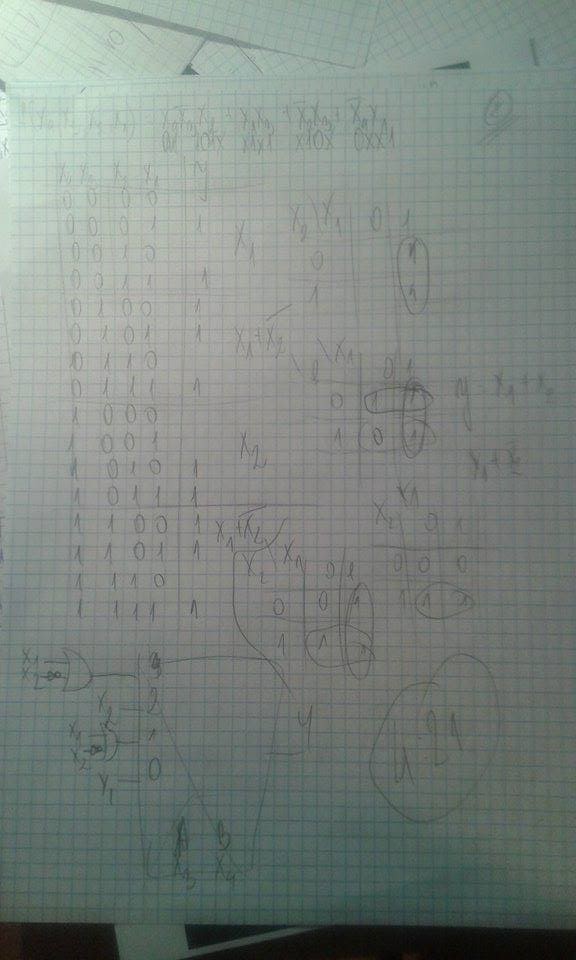


ł. fe: t
Wyszukiwarka
Podobne podstrony:
zadanie3 wykresy Próbkowanie sygnału xa z Ts1 x3(n) x2(n) x
f(X3,X2,X1) = TT m(0,2,4,6)
y = (*! + x2 + x3) * (x4 + xa + x2) * (x3 + x4 + x3) * (x7 + x2) * (x3 + x4 + x3 + x2) y = (x3 + x2
J x9 x8 x7 x6 x5 *4 x3 x2 X1 33 32 31 3o 0 0 Q 0 0 0 0 0 0 0 0 0
Untitled Scanned 26 - 52 - y - ♦. x2 + x3 • x4 = X1 + x2 + x3 • x4 = - *! + *2 + x
MATEMATYKA026 b) Mianownik lej funkcji rozkładamy na czynniki: x4-x3 +3x2 = x2(x:-x + 3). Czynnikowi
Scan30010 (9.17) (9.18) )>1 = /(* 1, *3, X4) = *1*3 + *1*4 y2 =/(* 1, X2, x3) = XyX2 + XyX3 Na po
f4 X, X3 X4 + X, X2 X4 + X, X2 X3 ł X, x2 x3
2 (411) X3,X2X
x2 x3 x2 x3 różnica przemieszczeń [m] przemieszcenie
wykres 5 ĆW 5 x1[m ] x 1 (wariant 1) x 1 (wariant 2)
2 (1926) Zadania powtórzeniowe Zadania powtórzeniowe f 2x3 - 128 = 0 f 27 + x3 = 0 C) I b) 2 [
I. WYRAŻENIA ALGEBRAICZNE ■ dzielenia wielomianu 7. Rozłóż na czynniki wielomian W (x)=x3+x2- 3
więcej podobnych podstron